6 Inner Products Spaces

6.1 Inner Products and Norms

Definition

Definition: Inner product [core]

Let $\mathsf{V}$ be a vector space over field $F$. An inner product on $\mathsf{V}$ is a function assigning each ordered pair of vectors $⟨x,y⟩$ in $\mathsf{V}\times \mathsf{V}$ a scalar $⟨x,y⟩\in F$,satisfying:

• $⟨x+z,y⟩=⟨x,y⟩+⟨z,y⟩$.
• $⟨cx,y⟩=c⟨x,y⟩$ for $c\in F$.
• $⟨x,y⟩=\overline{⟨y,x⟩}$ where the bar denotes complex conjugation.
• $⟨x,x⟩>0$ if $x\ne 0$

Note that:

• The 3rd one reduces to $⟨x,y⟩=⟨y,x⟩$ if $F=\mathbb{R}$
• The 1st and 2nd parts simply require that the inner product be linear in the first component, (and conjugate linear in the second component).
• It's easily shown that if $a_1,a_2,\cdots ,a_n\in F$ and $y,v_1,v_2,\cdots ,v_n\in \mathsf{V}$, then$$⟨\sum _{i=1}^n{a}_i{v}_i,y⟩=\sum _{i=1}^n{a}_i⟨v_i,y⟩.$$

The idea of distance or length is missing. Therefore we need a richer structure, the so-called inner product space structure, by adding a new inner product function.

Example 6.1.1

Example 1 For $x=(a_1,a_2,\dots ,a_n)$ and $y=(b_1,b_2,\dots ,b_n)$ in ${\mathsf{F}}^n$, define

$$⟨x,y⟩=\sum _{i=1}^n{a}_i\overline{b_i}$$

The verification that $⟨\cdot ,\cdot ⟩$ satisfies conditions the 1st through (4th) is easy. For example, if $z=(c_1,c_2,\dots ,c_n)$, we have for (a)

$$\begin{array}{rl}⟨x+z,y⟩& =\sum _{i=1}^n(a_i+c_i)\overline{b_i}=\sum _{i=1}^n{a}_i\overline{b_i}+\sum _{i=1}^n{c}_i\overline{b_i}\\ & =⟨x,y⟩+⟨z,y⟩\end{array}$$

Thus, for $x=(1+i,4)$ and $y=(2-3i,4+5i)$ in ${\mathbb{C}}^2$,

$$⟨x,y⟩=(1+i)(2+3i)+4(4-5i)=15-15i.$$

The inner product in Example 1 is called the standard inner product on ${\mathsf{F}}^n$. When $F=\mathbb{R}$ the conjugations are not needed, and in early courses this standard inner product is usually called the dot product and is denoted by $x\cdot y$ instead of $⟨x,y⟩$.

Example 6.1.2

If $⟨x,y⟩$ is any inner product on a vector space $\mathsf{V}$ and $r>0$, define another inner product by $⟨x,y{⟩}^{\prime }=r⟨x,y⟩$. If $r\le 0$, then the 4th one of definition for inner product would not hold.

Example 6.1.3

Let $\mathsf{V}=\mathsf{C}([0,1])$, the vector space of real-valued continuous functions on $[0,1]$. For $f,g\in \mathsf{V}$, define

$$⟨f,g⟩={\int }_0^{1}f(t)g(t)dt.$$

• Since the proceding integral is linear in $f$, the 1st and the 2nd parts are immediate.
• the 3rd one is trival (real-value).
• If $f\not\equiv 0$, then $f^2$ is bounded away from zero on some subinterval of $[0,1]$ (continuity is used here), and hence $⟨f,f⟩={\int }_0^1[f(t){]}^2\mathrm{d}t>0$.

conjugate transpose

Definition: conjugate transpose

Let $A\in {\mathsf{M}}_{m\times n}(F)$. Define the conjugate transpose or adjoint of $A$ as the $n\times m$ matrix $A^{\ast }$ such that $(A^{\ast }{)}_{ij}={\bar{A}}_{ji}$ for all $i,j$.

Example 6.1.4

If

$$A=\left[\begin{array}{cc}i& 1+2i\\ 2& 3+4i\end{array}\right],$$

then

$$A^{\ast }=\left[\begin{array}{cc}-i& 2\\ 1-2i& 3-4i\end{array}\right].$$

Notice that:

• if $x,y$ are viewed as column vector in ${\mathsf{F}}^n$, then $⟨\mathit{x},\mathit{y}⟩={\mathit{y}}^{\ast }\mathit{x}$.
• The conjugate transpose of a matrix plays a very important role in the remainder of this chapter. In the case that $A$ has only real entries, $A^{\ast }$ is simply the transpose of $A$.

Example 6.1.5

Let $\mathsf{V}={\mathsf{M}}_{n\times n}(F)$, and define $⟨A,B⟩=\mathrm{tr}(B^{\ast }A)$ for $A,B\in \mathsf{V}$. (Recall that the trace of a matrix $A$ is defined by $\mathrm{tr}(A)=\sum _{i=1}^n{A}_{ii}$.) We verify that the 1st and 4th of the definition of inner product hold and leave (b) and (c) to the reader. For this purpose, let $A,B,C\in \mathsf{V}$. Then

$$\begin{array}{rl}⟨A+B,C⟩& =\mathrm{tr}(C^{\ast }(A+B))=\mathrm{tr}(C^{\ast }A+C^{\ast }B)\\ & =\mathrm{tr}(C^{\ast }A)+\mathrm{tr}(C^{\ast }B)=⟨A,C⟩+⟨B,C⟩.\end{array}$$

Also

$$\begin{array}{rl}⟨A,A⟩& =\mathrm{tr}(A^{\ast }A)=\sum (A^{\ast }A{)}_{ii}=\sum _{i=1}^n\sum _{k=1}^n(A^{\ast }{)}_{ik}{A}_{ki}\\ & =\sum _{i=1}^n\sum _{k=1}^n\overline{A_{ki}}{A}_{ki}=\sum _{i=1}^n\sum _{k=1}^n|A_{ki}{|}^2.\end{array}$$

Now if $A\ne \mathbf{0}$, then $A_{ki}\ne 0$ for some $k$ and $i$. So $⟨A,A⟩>0$.

inner product space

The inner product on ${\mathsf{M}}_{n\times n}(F)$ in Example 6.1.5 is called the Frobenius inner product.

A vector space $\mathsf{V}$ over $F$ endowed with a specific inner product is called an inner product space. If $F=\mathbb{C}$, we call $\mathsf{V}$ a complex inner product space, whereas if $F=\mathbb{R}$, we call $\mathsf{V}$ a real inner product space.

For the remainder of this chapter, ${\mathsf{F}}^n$ denotes the inner product space with the standard inner product as defined in Example 6.1.1. Likewise, ${\mathsf{M}}_{n\times n}(F)$ denotes the inner product space with the Frobenius inner product as defined in Example 6.1.5. The reader is cautioned that two distinct inner products on a given vector space yield two distinct inner product spaces. For instance, it can be shown that both

$$⟨f(x),g(x){⟩}_1={\int }_{-1}^{1}f(t)g(t)\mathrm{d}t\text{and}⟨f(x),g(x){⟩}_2={\int }_0^{1}f(t)g(t)\mathrm{d}t$$

are inner products on the vector space $\mathsf{P}(\mathbb{R})$. Even though the underlying vector space is the same, however, these two inner products yield two different inner product spaces. For example, the polynomials $f(x)=x$ and $g(x)=x^2$ are orthogonal in the second inner product space, but not in the first. About orthogonal, introduce it later.

A very important inner product space that resembles $\mathsf{C}([0,1])$ is the space $\mathsf{H}$ of continuous complex-valued functions defined on the interval $[0,2\pi ]$ with the inner product

$$⟨f,g⟩=\frac{1}{2\pi }{\int }_0^{2\pi }f(t)\overline{g(t)}\mathrm{d}t.$$

Show that the vector space $\mathsf{H}$ with $⟨\cdot ,\cdot ⟩$ defined above is an inner product space.

Check the condition one by one.

$$\begin{array}{rl}& ⟨f+h,g⟩=\frac{1}{2\pi }{\int }_0^{2\pi }(f(t)+h(t))\overline{g(t)}\mathrm{d}t\\ =& \frac{1}{2\pi }{\int }_0^{2\pi }f(t)\overline{g(t)}\mathrm{d}t+\frac{1}{2\pi }{\int }_0^{2\pi }h(t)\overline{g(t)}\mathrm{d}t=⟨f,g⟩+⟨h,g⟩.\\ & ⟨cf,g⟩=\frac{1}{2\pi }{\int }_0^{2\pi }(cf(t))\overline{g(t)}\mathrm{d}t=c\frac{1}{2\pi }{\int }_0^{2\pi }f(t)\overline{g(t)}\mathrm{d}t=c⟨f,g⟩.\\ & ⟨f,g⟩=\overline{⟨g,f⟩}.\\ & ⟨f,f⟩=\frac{1}{2\pi }{\int }_0^{2\pi }|f(t){|}^2\mathrm{d}t>0\text{if }f\not\equiv 0.\end{array}$$

At this point, we mention a few facts about integration of complex-valued functions.

1. the imaginary number $i$ can be treated as a constant under the integration sign.
2. every complex-valued function $f$ may be written as $f=f_1+i{f}_2$, where $f_1$ and $f_2$ are real-valued functions. Thus we have

$$\int f=\int f_1+i\int f_2\text{and}\overline{\int f}=\int \overline{f}.$$

Theorem 6.1

Let $V$ be an inner product space. Then for $x,y,z\in V$ and $c\in F$, the following statements are true.

• $⟨x,y+z⟩=⟨x,y⟩+⟨x,z⟩$.
• $⟨x,cy⟩=c⟨x,y⟩$.
• $⟨x,0⟩=⟨0,x⟩=0$.
• $⟨x,x⟩=0$ if and only if $x=0$.
• If $⟨x,y⟩=⟨x,z⟩$ for all $x\in V$, then $y=z$.

The 1st and 2nd of Theorem 6.1 show that the inner product is conjugate linear in the second component.

Norms

Definition: Norm / Length

Let $\mathsf{V}$ be an inner product space. For $x\in \mathsf{V}$, we define the norm or length of $x$ by $\parallel x\parallel =\sqrt{⟨x,x⟩}$.

Example 6.1.6

Let $\mathsf{V}={\mathsf{F}}^n$. If $x=(a_1,a_2,\dots ,a_n)$, then

$$\parallel x\parallel =\parallel (a_1,a_2,\dots ,a_n)\parallel =\sqrt{\sum _{i=1}^n|a_i{|}^2}$$

is the Euclidean definition of length. Note that if $n=1$, we have $\parallel a\parallel =|a|$.

Theorem 6.2

Theorem 6.2

Let $\mathsf{V}$ be an inner product space over $F$. Then for all $x,y\in \mathsf{V}$ and $c\in F$, the following statements are true.

• $\parallel cx\parallel =|c|\cdot \parallel x\parallel$.
• $\parallel x\parallel =0$ if and only if $x=0$. In any case, $\parallel x\parallel \ge 0$.
• (Cauchy-Schwarz Inequality) $|⟨x,y⟩|\le \parallel x\parallel \cdot \parallel y\parallel$.
• (Triangle Inequality) $\parallel x+y\parallel \le \parallel x\parallel +\parallel y\parallel$.

Example 6.1.7

For ${\mathsf{F}}^n$, we may apply 3rd and 4th of Theorem 6.2 to the standard inner product to obtain the following well-known inequalities:

$$\left|\sum _{i=1}^n{a}_i{\overline{b}}_i\right|\le {\left[\sum _{i=1}^n{\left|a_i\right|}^2\right]}^{1/2}{\left[\sum _{i=1}^n{\left|b_i\right|}^2\right]}^{1/2}$$

and

$${\left[\sum _{i=1}^n{|a_i+b_i|}^2\right]}^{1/2}\le {\left[\sum _{i=1}^n{\left|a_i\right|}^2\right]}^{1/2}+{\left[\sum _{i=1}^n{\left|b_i\right|}^2\right]}^{1/2}.$$

Orthogonal [core]

Definitions: orthogonal & orthonormal

Let $\mathsf{V}$ be an inner product space. Vectors $x$ and $y$ in $\mathsf{V}$ are orthogonal (perpendicular) if $⟨x,y⟩=0$.

A subset $S$ of $\mathsf{V}$ is orthogonal if any two distinct vectors in $S$ are orthogonal. A vector $x$ in $\mathsf{V}$ is a unit vector if $\parallel x\parallel =1$. Finally, a subset $S$ of $\mathsf{V}$ is orthonormal if $S$ is orthogonal and consists entirely of unit vectors.

Note that if $S=\{v_1,v_2,\dots \}$ (infinite dimension), then $S$ is orthonormal if and only if $⟨v_i,v_j⟩={\delta }_{ij}$, where ${\delta }_{ij}$ denotes the Kronecker delta. Also, observe that multiplying vectors by nonzero scalars does not affect their orthogonality and that if $x$ is any nonzero vector, then $(1/\parallel x\parallel )x$ is a unit vector. The process of multiplying a nonzero vector by the reciprocal of its length is called normalizing.

Example 6.1.8

In ${\mathsf{F}}^3$, $\{(1,1,0),(1,-1,1),(-1,1,2)\}$ is an orthogonal set of nonzero vectors, but it is not orthonormal; however, if we normalize the vectors in the set, we obtain the orthonormal set

$$\{\frac{1}{\sqrt{2}}(1,1,0),\frac{1}{\sqrt{3}}(1,-1,1),\frac{1}{\sqrt{6}}(-1,1,2)\}.$$

Example 6.1.9

Recall the inner product space $\mathsf{H}$ (defined above). We introduce an important orthonormal subset $S$ of $\mathsf{H}$.

For what follows, $i$ is the imaginary number such that $i^2=-1$. For any integer $n$, let $f_n(t)=e^{int}$, where $0\le t\le 2\pi$. (Recall that $e^{int}=\cos nt+i\sin nt$.)

Now define $S=\{f_n:n\text{ is an integer}\}$. Clearly $S$ is a subset of $\mathsf{H}$. Using the property that $e^{it}=e^{-it}$ for every real number $t$, we have, for $m\ne n$,

$$⟨f_m,f_n⟩=\frac{1}{2\pi }{\int }_0^{2\pi }{e}^{imt}{e}^{-int}dt=\frac{1}{2\pi }{\int }_0^{2\pi }{e}^{i(m-n)t}dt=0.$$

Also,

$$⟨f_n,f_n⟩=\frac{1}{2\pi }{\int }_0^{2\pi }1dt=1.$$

In other words, $⟨f_m,f_n⟩={\delta }_{mn}$, the Kronecker delta.

---

6.2 The Gram-Schmidt Orthogonalization Process and Orthogonal Complements

Orthonormal basis

Definition: orthonormal basis

Let $\mathsf{V}$ be an inner product space. A subset of $\mathsf{V}$ is an orthonormal basis for $\mathsf{V}$ if it is an ordered basis that is orthonormal.

Example 6.2.1

The standard ordered basis for ${\mathsf{F}}^n$ is an orthonormal basis for ${\mathsf{F}}^n$.

Example 6.2.2

The set $\{(1/\sqrt{5},2/\sqrt{5}),(2/\sqrt{5},-1/\sqrt{5})\}$ is an orthonormal basis for ${\mathbb{R}}^2$.

Theorem 6.3

Theorem 6.3

Let $\mathsf{V}$ be an inner product space and $S=\{v_1,v_2,\dots ,v_k\}$ be an orthogonal subset of $\mathsf{V}$ consisting of nonzero vectors. If $y\in \mathrm{span}(S)$, then

$$y=\sum _{i=1}^k{a}_i{v}_i,$$

where

$$a_i=\frac{⟨y,v_i⟩}{\parallel v_i{\parallel }^2}\text{for }i=1,2,\dots ,k.$$

Corollary of Theorem 6.3

Corollary

1. If, in addition to the hypotheses of Theorem 6.3, $S$ is orthonormal and $y\in \mathrm{span}(S)$, then

$$y=\sum _{i=1}^k⟨y,v_i⟩v_i.$$

2. Let $V$ be an inner product space, and let $S$ be an orthogonal subset of $V$ consisting of nonzero vectors. Then $S$ is linearly independent.

For Corollary 1: If $\mathsf{V}$ possesses a finite orthonormal basis, then Corollary 1 allows us to compute the coefficients in a linear combination very easily.

Example 6.2.3

By Corollary 2, the orthonormal set

$$\{\frac{1}{\sqrt{2}}(1,1,0),\frac{1}{\sqrt{3}}(1,-1,1),\frac{1}{\sqrt{6}}(-1,1,2)\}$$

obtained in Example 6.1.8 is an orthonormal basis for ${\mathbb{R}}^3$. Let $x=(2,1,3)$. The coefficients given by Corollary 1 to Theorem 6.3 that express $x$ as a linear combination of the basis vectors are

$$a_1=\frac{⟨x,v_1⟩}{\parallel v_1{\parallel }^2}=\frac{2+1}{\sqrt{2}},a_2=\frac{2-1+3}{\sqrt{3}},a_3=\frac{-2+1+6}{\sqrt{6}}.$$

As a check, we have

$$(2,1,3)=a_1(1,1,0)+a_2(1,-1,1)+a_3(-1,1,2).$$

Gram-Schmidt process

Before stating this theorem, let us consider a simple case. Suppose that $\{w_1,w_2\}$ is a linearly independent subset of an inner product space (and hence a basis for some two-dimensional subspace). We want to construct an orthogonal set from $\{w_1,w_2\}$ that spans the same subspace.

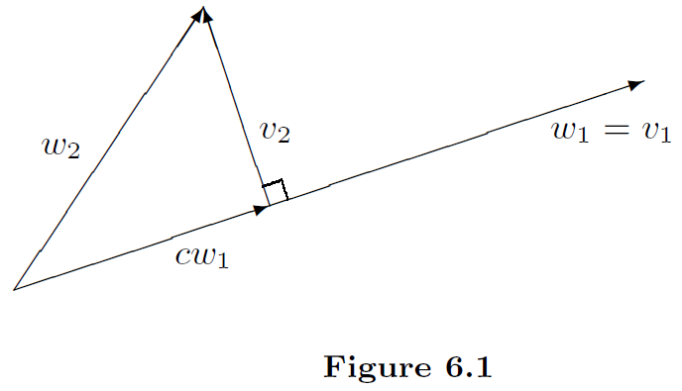
Figure 6.1 suggests that the set $\{v_1,v_2\}$, where $v_1=w_1$ and $v_2=w_2-c{w}_1$, has this property if $c$ is chosen so that $v_2$ is orthogonal to $w_1$. To find $c$, we solve

$$0=⟨v_2,w_1⟩=⟨w_2-c{w}_1,w_1⟩=⟨w_2,w_1⟩-c⟨w_1,w_1⟩.$$

So

$$c=\frac{(w_2,w_1)}{\parallel w_1{\parallel }^2}.$$

Thus

$$v_2=w_2-\frac{⟨w_2,w_1⟩}{\parallel w_1{\parallel }^2}{w}_1$$

Theorem 6.4: Gram-Schmidt process [core]

Let $\mathsf{V}$ be an inner product space and $S=\{w_1,w_2,\dots ,w_n\}$ be a linearly independent subset of $\mathsf{V}$. Define $S^{\prime }=\{v_1,v_2,\dots ,v_n\}$, where $v_1=w_1$, and for $2\le k\le n$,

$$v_k=w_k-\sum _{j=1}^{k-1}\frac{⟨w_k,v_j⟩}{\parallel v_j{\parallel }^2}{v}_j.$$

Then $S^{\prime }$ is an orthogonal set of nonzero vectors such that $\mathrm{span}(S^{\prime })=\mathrm{span}(S)$.

This construction of $\{v_1,v_2,\cdots ,v_n\}$ by the use of Theorem 6.4 is called the Gram-Schmidt process.

Example 6.2.4 [core]

In ${\mathbb{R}}^4$, let $w_1=(1,0,1,0)$, $w_2=(1,1,1,1)$, and $w_3=(0,1,2,1)$. Then $\{w_1,w_2,w_3\}$ is linearly independent. We use the Gram-Schmidt process to compute orthogonal vectors $v_1,v_2,v_3$, then normalize them to obtain an orthonormal set.

Take $v_1=w_1=(1,0,1,0)$. Then

$$v_2=w_2-\frac{⟨w_2,v_1⟩}{\parallel v_1{\parallel }^2}{v}_1=(1,1,1,1)-\frac{2}{2}(1,0,1,0)=(0,1,0,1).$$

Finally,

$$\begin{array}{rl}{v}_3& =w_3-\frac{⟨w_3,v_1⟩}{\parallel v_1{\parallel }^2}{v}_1-\frac{⟨w_3,v_2⟩}{\parallel v_2{\parallel }^2}{v}_2\\ & =(0,1,2,1)-\frac{2}{2}(1,0,1,0)-\frac{2}{2}(0,1,0,1)=(-1,0,1,0).\end{array}$$

Normalization yields the orthonormal basis $\{u_1,u_2,u_3\}$ where

$$\begin{array}{rl}{u}_1& =\frac{v_1}{\parallel v_1\parallel }=\frac{1}{\sqrt{2}}(1,0,1,0),\\ u_2& =\frac{v_2}{\parallel v_2\parallel }=\frac{1}{\sqrt{2}}(0,1,0,1),\\ u_3& =\frac{v_3}{\parallel v_3\parallel }=(-1,0,1,0).\end{array}$$

---

Example 6.2.5

Let $\mathsf{V}=\mathsf{P}(\mathbb{R})$ with the inner product

$$⟨f(x),g(x)⟩={\int }_{-1}^{1}f(t)g(t)\mathrm{d}t,$$

and consider the subspace ${\mathsf{P}}_2(\mathbb{R})$ with the standard ordered basis $\beta =\{1,x,x^2\}$. We use the Gram-Schmidt process to replace $\beta$ with an orthogonal basis $\{v_1,v_2,v_3\}$ for ${\mathsf{P}}_2(\mathbb{R})$, then obtain an orthonormal basis.

Take $v_1=1$. Then ${\Vert v_1\Vert }^2={\int }_{-1}^1{1}^2\mathrm{d}t=2$, and $⟨x,v_1⟩={\int }_{-1}^{1}t\cdot 1\mathrm{d}t=0$. Thus

$$v_2=x-\frac{⟨v_1,x⟩}{{\Vert v_1\Vert }^2}=x-\frac{0}{2}=x.$$

Furthermore,

$$⟨x^2,v_1⟩={\int }_{-1}^1{t}^2\cdot 1\mathrm{d}t=\frac{2}{3}\text{ and }⟨x^2,v_2⟩={\int }_{-1}^1{t}^2\cdot t\mathrm{d}t=0$$

Therefore

$$\begin{array}{rl}{v}_3& =x^2-\frac{⟨x^2,v_1⟩}{{\Vert v_1\Vert }^2}{v}_1-\frac{⟨x^2,v_2⟩}{{\Vert v_2\Vert }^2}{v}_2\\ & =x^2-\frac{1}{3}\cdot 1-0\cdot x\\ & =x^2-\frac{1}{3}.\end{array}$$

We conclude that $\{1,x,x^2-\frac{1}{3}\}$ is an orthogonal basis for ${\mathsf{P}}_2(R)$.

To obtain an orthonormal basis, we normalize $v_1,v_2$, and $v_3$ to obtain

$$\begin{array}{rl}& u_1=\frac{1}{\sqrt{{\int }_{-1}^1{1}^2\mathrm{d}t}}=\frac{1}{\sqrt{2}}\\ & u_2=\frac{x}{\sqrt{{\int }_{-1}^1{t}^2\mathrm{d}t}}=\sqrt{\frac{3}{2}}x\end{array}$$

and similarly,

$$u_3=\frac{v_3}{\Vert v_3\Vert }=\sqrt{\frac{5}{8}}(3x^2-1).$$

Thus $\{u_1,u_2,u_3\}$ is the desired orthonormal basis for ${\mathsf{P}}_2(\mathbb{R})$.

If we continue applying the Gram-Schmidt orthogonalization process to the basis $\{1,x,x^2,\dots \}$ for $\mathsf{P}(\mathbb{R})$, we obtain an orthogonal basis whose elements are called the Legendre polynomials. The orthogonal polynomials $v_1,v_2$, and $v_3$ in Example 6.2.5 are the first three Legendre polynomials.

Theorem 6.5

Theorem 6.5

Let $\mathsf{V}$ be a nonzero finite-dimensional inner product space. Then $\mathsf{V}$ has an orthonormal basis $\beta$. Furthermore, if $\beta =\{v_1,v_2,\dots ,v_n\}$ and $x\in \mathsf{V}$, then

$$x=\sum _{i=1}^n⟨x,v_i⟩v_i.$$

Example 6.2.6

We use Theorem 6.5 to represent the polynomial $f(x)=1+2x+3x^2$ as a linear combination of the vectors in the orthonormal basis $\{u_1,u_2,u_3\}$ for ${\mathsf{P}}_2(\mathbb{R})$ obtained in Example 6.2.5. Observe that:

$$\begin{array}{r}⟨f(x),u_1⟩={\int }_{-1}^1\frac{1}{\sqrt{2}}(1+2t+3t^2)u_1(t)\mathrm{d}t=2\sqrt{2},\\ ⟨f(x),u_2⟩={\int }_{-1}^1\sqrt{\frac{3}{2}}t(1+2t+3t^2)u_1(t)\mathrm{d}t=\frac{2\sqrt{6}}{3},\\ ⟨f(x),u_3⟩={\int }_{-1}^1(1+2t+3t^2)u_1(t)\mathrm{d}t=\frac{2\sqrt{10}}{5}.\end{array}$$

Therefore,

$$f(x)=2\sqrt{2}{u}_1+\frac{2\sqrt{6}}{3}{u}_2+\frac{2\sqrt{10}}{5}{u}_3.$$

Corollary of Theorem 6.5

Corollary

Let $\mathsf{V}$ be a finite-dimensional inner product space with an orthonormal basis $\beta =\{v_1,v_2,\dots ,v_n\}$. Let $\mathsf{T}$ be a linear operator on $V$, and let $A=[\mathsf{T}{]}_{\beta }$. Then for any $i$ and $j$,

$$A_{ij}=⟨\mathsf{T}(v_j),v_i⟩.$$

Fourier coefficients [core]

Definition: Fourier coefficients

Let $\beta$ be an orthonormal subset (possibly infinite) of an inner product space $\mathsf{V}$, and let $x\in \mathsf{V}$. We define the Fourier coefficients of $x$ relative to $\beta$ to be the scalars $⟨x,y⟩$ where $y\in \beta$.

Example 6.2.7

Let $S=\{e^{int}:n\text{ is an integer}\}$. In Example 6.1.9, $S$ was shown to be an orthonormal set in $\mathsf{H}$. We compute the Fourier coefficients of $f(t)=t$ relative to $S$. Using integration by parts, for $n\ne 0$,

$$⟨f,f_n⟩=\frac{1}{2\pi }{\int }_0^{2\pi }t{e}^{-int}\mathrm{d}t=\frac{i}{n},$$

and for $n=0$,

$$⟨f,1⟩=\frac{1}{2\pi }{\int }_0^{2\pi }t\mathrm{d}t=\pi .$$

Orthogonal complement

Definition: orthogonal complement

Let $S$ be a nonempty subset of an inner product space $\mathsf{V}$. We define $S^{\perp }$ (read "S perp") to be the set of all vectors in $\mathsf{V}$ that are orthogonal to every vector in $S$; that is,

$$S^{\perp }=\{x\in \mathsf{V}:⟨x,y⟩=0\text{ for all }y\in S\}.$$

The set $S^{\perp }$ is called the orthogonal complement of $S$. It is easily seen that $S^{\perp }$ is a subspace of $\mathsf{V}$ for any subset $S$ of $\mathsf{V}$.

Example 6.2.8

The reader should verify that $\{0{\}}^{\perp }=\mathsf{V}$ and ${\mathsf{V}}^{\perp }=\{0\}$ for any inner product space $\mathsf{V}$.

Example 6.2.9

If $\mathsf{V}={\mathbb{R}}^3$ and $S=\{e_3\}$, then $S^{\perp }$ equals the xy-plane.

Let $S_0=\{{\mathit{x}}_0\}$, where ${\mathit{x}}_0$ is a nonzero vector in ${\mathbb{R}}^3$. Describe $S^{\perp }$ geometrically. Now suppose $S=\{{\mathit{x}}_1,{\mathit{x}}_2\}$ is a linearly independent subset of ${\mathbb{R}}^3$. Describe $S^{\perp }$ geometrically.

We may think of $S^{\perp }$ as the plane orthogonal to ${\mathit{x}}_0$, and if $S$ spans a plane, then $S^{\perp }$ is the line orthogonal to that plane.

Consider the problem in ${\mathbb{R}}^3$ of finding the distance from a point $P$ to a plane $\mathsf{W}$. (See Figure 6.2.) If we let $y$ be the vector determined by $0$ and $P$, we may restate the problem as follows:

Determine the vector $\mathit{u}$ in $\mathsf{W}$ that is "closest" to $y$. The desired distance is clearly given by $\parallel \mathit{y}-\mathit{u}\parallel$. Notice from the figure that the vector $\mathit{z}=\mathit{y}-\mathit{u}$ is orthogonal to every vector in $\mathsf{W}$, so $\mathit{z}\in {\mathsf{W}}^{\perp }$.

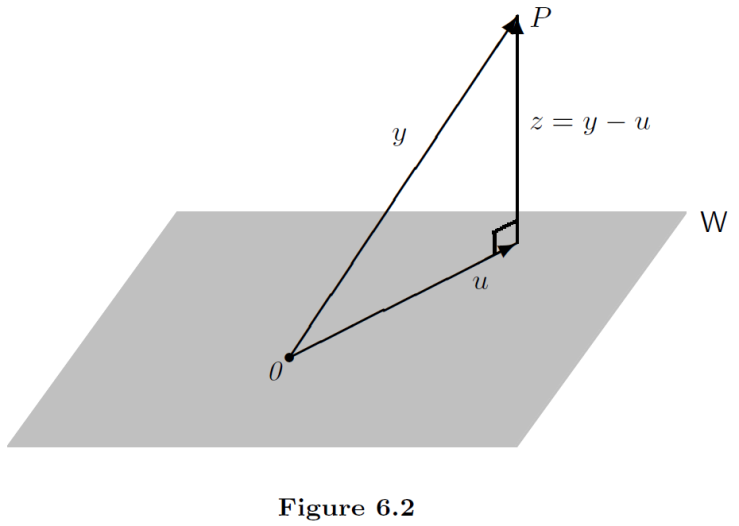
Orthogonal projection

Theorem 6.6

Let $\mathsf{W}$ be a finite-dimensional subspace of an inner product space $\mathsf{V}$, and let $y\in \mathsf{V}$. Then there exist unique vectors $u\in \mathsf{W}$ and $z\in {\mathsf{W}}^{\perp }$ such that $y=u+z$. Furthermore, if $\{v_1,v_2,\dots ,v_k\}$ is an orthonormal basis for $\mathsf{W}$, then

$$u=\sum _{i=1}^k⟨y,v_i⟩v_i.$$

P.S. From Corollary 1 of Theorem 6.3:

$$u=\sum _{i=1}^k⟨u,v_i⟩v_i.$$

Corollary

In the notation of Theorem 6.6, the vector $u$ is the unique vector in $\mathsf{W}$ that is "closest" to $y$; that is, for any $x\in \mathsf{W}$, $\parallel y-x\parallel \ge \parallel y-u\parallel$, and this inequality is an equality if and only if $x=u$.

The vector $u$ is called the orthogonal projection of $y$ onto $\mathsf{W}$.

Example 6.2.10

Let $\mathsf{V}={\mathsf{P}}_3(\mathbb{R})$ with inner product

$$⟨f(x),g(x)⟩={\int }_{-1}^{1}f(t)g(t)\mathrm{d}t\text{for all }f,g\in \mathsf{V}.$$

We compute the orthogonal projection $f_1(x)$ of $f(x)=x^3$ on ${\mathsf{P}}_2(\mathbb{R})$.

By Example 6.2.5, $\{u_1,u_2,u_3\}$ is an orthonormal basis for ${\mathsf{P}}_2(\mathbb{R})$ with

$$\{\frac{1}{\sqrt{2}},\sqrt{\frac{3}{2}}x,\sqrt{\frac{5}{8}}(3x^2-1)\}$$

Computing inner products:

$$⟨f,u_1⟩=0,⟨f,u_2⟩={\int }_{-1}^1{t}^3\sqrt{\frac{3}{2}}t\mathrm{d}t=\frac{\sqrt{6}}{5},⟨f,u_3⟩=0.$$

Hence

$$f_1(x)=\sum _{i=1}^3⟨f(x),u_i⟩u_i=\frac{3}{5}x.$$

Theorem 6.7

Theorem 6.7

Suppose that $S=\{v_1,v_2,\dots ,v_k\}$ is an orthonormal set in an $n$-dimensional inner product space $\mathsf{V}$. Then

• $S$ can be extended to an orthonormal basis $\{v_1,v_2,\dots ,v_k,v_{k+1},\dots ,v_n\}$ for $\mathsf{V}$.

• If $\mathsf{W}=\mathrm{span}(S)$, then

$$S_1=\{v_{k+1},v_{k+2},\dots ,v_n\}$$

is an orthonormal basis for ${\mathsf{W}}^{\perp }$.

• If $\mathsf{W}$ is any subspace of $\mathsf{V}$, then

$$\dim (\mathsf{V})=\dim (\mathsf{W})+\dim ({\mathsf{W}}^{\perp }).$$

Example 6.2.11

Let $\mathsf{W}=\mathrm{span}(\{e_1,e_2\})$ in ${\mathsf{F}}^3$. Then $x=(a,b,c)\in {\mathsf{W}}^{\perp }$ if and only if

$$⟨x,e_1⟩=0,⟨x,e_2⟩=0.$$

So $x=(0,0,c)$, and therefore ${\mathsf{W}}^{\perp }=\mathrm{span}(\{e_3\})$. Thus $e_3\in {\mathsf{W}}^{\perp }$ and from 3rd claim of Theorem 6.7, that $\dim ({\mathsf{W}}^{\perp })=3-2=1$.