Test in the class

Test1: Flow Loop Design

It has been decided to conduct a two-phase flow experiment at the given void fraction and mass flux. During the experiment, there will be a pressure drop in the system due to the liquid single-phase flow and two-phase flow. Estimation of the pressure drop is essential to select right equipment such as pump. To select the pump, liquid flow rate and total head loss are required. In the current simplified example, the procedure for pump selection is reviewed.

Given Key Information

• Void fraction：$⟨\alpha ⟩=0.75$
• Mass flux $G=1000\mathrm{kg}/(\mathrm{m}\cdot \mathrm{s})$
• Pressure condition： $P=0.1\mathrm{MPa}$
• Temperature condition：$T={20}^{\circ }\mathrm{C}$
• Diameter of the vertical pipe test section：$D_h=0.05\mathrm{m}$
• Height of the vertical pipe test section：$H=5.0\mathrm{m}$
• Diameter of the horizontal water piping system：$D=0.10\mathrm{m}$
• Length of the horizontal water piping system：$L=10\mathrm{m}$
• Liquid density：${\rho }_f=998\mathrm{kg}/{\mathrm{m}}^3$
• Gas density：${\rho }_g=1.17\mathrm{kg}/{\mathrm{m}}^3$
• Liquid dynamic viscosity ${\mu }_f=1.00\times {10}^{-3}\mathrm{Pa}\cdot \mathrm{s}$
• Gas dynamic viscosity：${\mu }_g=1.81\times {10}^{-5}\mathrm{Pa}\cdot \mathrm{s}$
• Gravity acceleration：$g=9.8\mathrm{m}/{\mathrm{s}}^2$
• Air－water surface tension：$\sigma =0.0727\mathrm{N}/\mathrm{m}$

Design Procedure

Step

1. Boundary conditions: $\alpha =0.75,G=1000\mathrm{kg}/({\mathrm{m}}^2\cdot \mathrm{s}),P=1.0\mathrm{MPa}$, Fluid system: Steam-water
2. Identify key flow parameters: $⟨j_g⟩$ and $⟨j_f⟩$
3. Total pressure drop in two-phase flow test section
   • Hydrostatic Pressure Drop: $\mathrm{\Delta }{P}_{\text{hydro}}$.
   • Frictional Pressure Drop: $\mathrm{\Delta }{P}_{\text{fric},2\mathrm{\Phi }}$
4. Total pressure drop in single-phase flow piping section
   • Frictional Pressure Drop: $\mathrm{\Delta }{P}_{\text{fric},1\mathrm{\Phi }}$
   • Valve Head Loss: $\mathrm{\Delta }{P}_{\text{valve}}=1\mathrm{m}$
5. Total pressure drop in flow loop & Find an appropriate pump in terms of pump head and pump flow rate

Assumptions

• Ignore the pressure loss in two-phase mixing section
• Ignore the pressure loss at the inlet and outlet sections
• Steam and water fluid compressibility is negligible.
• Void fraction change along the flow direction is negligible.

Q1-1

Write down the superficial gas and liquid velocity $⟨j_g⟩,⟨j_f⟩$ as function of mass flux $G$ , quality $⟨x⟩$ and phase densities ${\rho }_g,{\rho }_f$

Answer:

$$\begin{array}{rl}& ⟨j_g⟩=\frac{G⟨x⟩}{{\rho }_g}\\ & ⟨j_f⟩=\frac{G(1-⟨x⟩)}{{\rho }_f}\end{array}$$

Q1-2

Express the void fraction $⟨\alpha ⟩$, as a function of superficial gas $⟨j_g⟩$, velocity mixture volumetric flux $⟨j⟩$, distribution parameter $C_0$ and drift velocity $⟨⟨v_{gj}⟩⟩$ (drift-flux model)

Answer:

$$⟨\alpha ⟩=\frac{⟨j_g⟩}{C_0⟨j⟩+⟨⟨v_{gj}⟩⟩}$$

Q1-3

Use results of question 1 and drift-flux model to write the quality $⟨x⟩$ as an explicit function of distribution parameter $C_0$, drift velocity $⟨⟨v_{gj}⟩⟩$, void fraction $⟨\alpha ⟩$, mass flux $G$ ans phase densities ${\rho }_g,{\rho }_f$.

Answer:

$$⟨x⟩=\frac{{\rho }_g⟨\alpha ⟩}{G}(C_0⟨j⟩+⟨⟨v_{gj}⟩⟩)$$

not right

$$\begin{array}{rl}& ⟨j⟩=⟨j_g⟩+⟨j_f⟩=\frac{G⟨x⟩}{{\rho }_g}+\frac{G(1-⟨x⟩)}{{\rho }_f}\\ ⟹& ⟨x⟩=\frac{\frac{C_0}{{\rho }_f}+\frac{⟨⟨v_{gj}⟩⟩}{G}}{\frac{1}{⟨\alpha ⟩{\rho }_g}-\frac{C_0}{{\rho }_g}+\frac{C_0}{{\rho }_f}}\end{array}$$

Q1-4

Consider dispersed gas-liquid two-phase flows in a vertical pipe of radius $R$. Assume that the flow is symmetric to the pipe center line and assume the following distribution profiles for void fraction and mixture volumetric flux along the radial direction:

$$\begin{array}{}\text{(1)}& & \alpha (r)={\alpha }_0(1-{\left(\frac{r}{R}\right)}^n)\text{(2)}& & j(r)=j_0(1-{\left(\frac{r}{R}\right)}^m)\end{array}$$

where ${\alpha }_0$ and $j_0$ are peak void fraction and peak mixture volumetric flux at the pipe center, respectively; $r$ and $R$ are coordinates along radial direction and pipe radius, respectively. (1) Calculate $⟨\alpha ⟩$ and $⟨j⟩$ by integrating Eqs. (1) and (2) over the flow area. (2) Calculate $C_0$ through its definition.

$$C_0\equiv \frac{⟨\alpha j⟩}{⟨\alpha ⟩⟨j⟩}.$$

(3) Calculate the distribution parameter using $m=n=4$.

Answer:

1. Here

$$\begin{array}{rl}⟨\alpha ⟩& =\frac{1}{A}{\int }_A\alpha (r)\mathrm{d}A=\frac{1}{\pi R^2}{\int }_0^R\alpha (r)\mathrm{d}(\pi r^2)\\ & =\frac{2}{R^2}{\alpha }_0{\int }_0^R(r-\frac{r^{n+1}}{R^n})\mathrm{d}r=\frac{2}{R^2}{\alpha }_0(\frac{R^2}{2}-\frac{R^2}{n+2})\\ & =\frac{n{\alpha }_0}{n+2}.\\ ⟨j⟩& =\frac{1}{A}{\int }_{A}j(r)\mathrm{d}A=\frac{1}{\pi R^2}{\int }_0^{R}j(r)\mathrm{d}(\pi r^2)\\ & =\frac{2}{R^2}{j}_0{\int }_0^R(r-\frac{r^{m+1}}{R^m})\mathrm{d}r=\frac{2}{R^2}{j}_0(\frac{R^2}{2}-\frac{R^2}{(m+2)})\\ & =\frac{m{j}_0}{m+2}.\end{array}$$

$$\begin{array}{rl}⟨\alpha ⟩& =\frac{1}{A}{\int }_A\alpha (r)\mathrm{d}A=\frac{1}{\pi R^2}{\int }_0^{2\pi }{\int }_0^R\alpha (r)r\mathrm{d}r\mathrm{d}\theta =\frac{n{\alpha }_0}{n+2}.\\ ⟨j⟩& =\frac{1}{A}{\int }_{A}j(r)\mathrm{d}A=\frac{1}{\pi R^2}{\int }_0^{2\pi }{\int }_0^{R}j(r)r\mathrm{d}r\mathrm{d}\theta =\frac{m{j}_0}{m+2}.\end{array}$$

2. Here:

$$C_0\equiv \frac{⟨\alpha j⟩}{⟨\alpha ⟩⟨j⟩}=\frac{1}{⟨\alpha ⟩⟨j⟩A}{\int }_A\alpha (r)j(r)\mathrm{d}(\pi r^2)$$

$$\begin{array}{rl}{C}_0& \equiv \frac{⟨\alpha j⟩}{⟨\alpha ⟩⟨j⟩}=\frac{1}{⟨\alpha ⟩⟨j⟩A}{\int }_A\alpha (r)j(r)\mathrm{d}A\\ & =\frac{1}{⟨\alpha ⟩⟨j⟩A}{\int }_0^{2\pi }{\int }_0^R\alpha (r)j(r)r\mathrm{d}r\mathrm{d}\theta \\ & =\frac{2{\alpha }_0{j}_0}{⟨\alpha ⟩⟨j⟩R^2}{\int }_0^R(r-\frac{r^{n+1}}{R^n})(1-\frac{r^m}{R^m})\mathrm{d}r\\ & =\frac{2{\alpha }_0{j}_0}{⟨\alpha ⟩⟨j⟩R^2}{\int }_0^{R}r-\frac{r^{n+1}}{R^n}-\frac{r^{m+1}}{R^m}+\frac{r^{m+1+n}}{R^{n+m}}\mathrm{d}r\\ & =\frac{2{\alpha }_0{j}_0}{⟨\alpha ⟩⟨j⟩R^2}(\frac{R^2}{2}-\frac{R^2}{n+2}-\frac{R^2}{m+2}+\frac{R^2}{m+n+2})\\ & =\frac{2{\alpha }_0{j}_0}{⟨\alpha ⟩⟨j⟩}(\frac{1}{2}-\frac{1}{n+2}-\frac{1}{m+2}+\frac{1}{m+n+2})\\ & =\frac{2(m+2)(n+2)}{mn}(\frac{1}{2}-\frac{1}{n+2}-\frac{1}{m+2}+\frac{1}{m+n+2})\\ & =\frac{m+n+4}{m+n+2}\end{array}$$

4. Thus

$$m=n=4⟹C_0=1.2$$

Q1-5

Calculate the chum drift velocity value given by

$$⟨⟨v_{gj}⟩⟩=\sqrt{2}{\left(\frac{\mathrm{\Delta }\rho g\sigma }{{\rho }_f^2}\right)}^{0.25}.$$

at the atmospheric flow condition. Fluid properties at the atmospheric condition: air and water densities are $1.17\mathrm{kg}/{\mathrm{m}}^3$ and $998\mathrm{kg}/{\mathrm{m}}^3$, and the surface tension and gravity acceleration are $0.0727\mathrm{N}/\mathrm{m}$ and $9.8\mathrm{m}/{\mathrm{s}}^2$.

Answer:

$$⟨⟨v_{gj}⟩⟩=\sqrt{2}{\left(\frac{\mathrm{\Delta }\rho g\sigma }{{\rho }_f^2}\right)}^{0.25}\approx 0.231\mathrm{m}/\mathrm{s}.$$

Q1-6

Calculate the quality for air water flow at void fraction of $0.75(⟨\alpha ⟩=0.75)$ atmospheric condition. Mass flux is $1000\mathrm{kg}/({\mathrm{m}}^2\cdot \mathrm{s})$. Use the values of drift velocity and distribution parameter in Questions 4 and 5. Fluid properties at the atmospheric condition: air and water densities are $1.17\mathrm{kg}/{\mathrm{m}}^3$ and $998\mathrm{kg}/{\mathrm{m}}^3$. Use the following equation.

$$⟨x⟩=\frac{\frac{C_0}{{\rho }_f}+\frac{⟨\left(v_{\mathrm{gi}}\right)⟩}{G}}{\frac{1}{⟨\alpha ⟩{\rho }_g}-\frac{C_0}{{\rho }_g}+\frac{C_0}{{\rho }_f}}$$

Answer:

$$⟨x⟩=\frac{\frac{C_0}{{\rho }_f}+\frac{⟨⟨v_{gj}⟩⟩}{G}}{\frac{1}{⟨\alpha ⟩{\rho }_g}-\frac{C_0}{{\rho }_g}+\frac{C_0}{{\rho }_f}}\approx 0.0124$$

Q1-7

Use the calculated quality $⟨x⟩=0.0124$ to obtain gas and liquid superficial velocity at mass flux of $1000\mathrm{kg}/({\mathrm{m}}^2\mathrm{s})$. The equations on question1 can be used.

Answer:

$$\begin{array}{rl}& ⟨j_g⟩=\frac{G⟨x⟩}{{\rho }_g}\approx 10.6\mathrm{m}/\mathrm{s}\\ & ⟨j_f⟩=\frac{G(1-⟨x⟩)}{{\rho }_f}\approx 0.990\mathrm{m}/\mathrm{s}.\end{array}$$

Q1-8

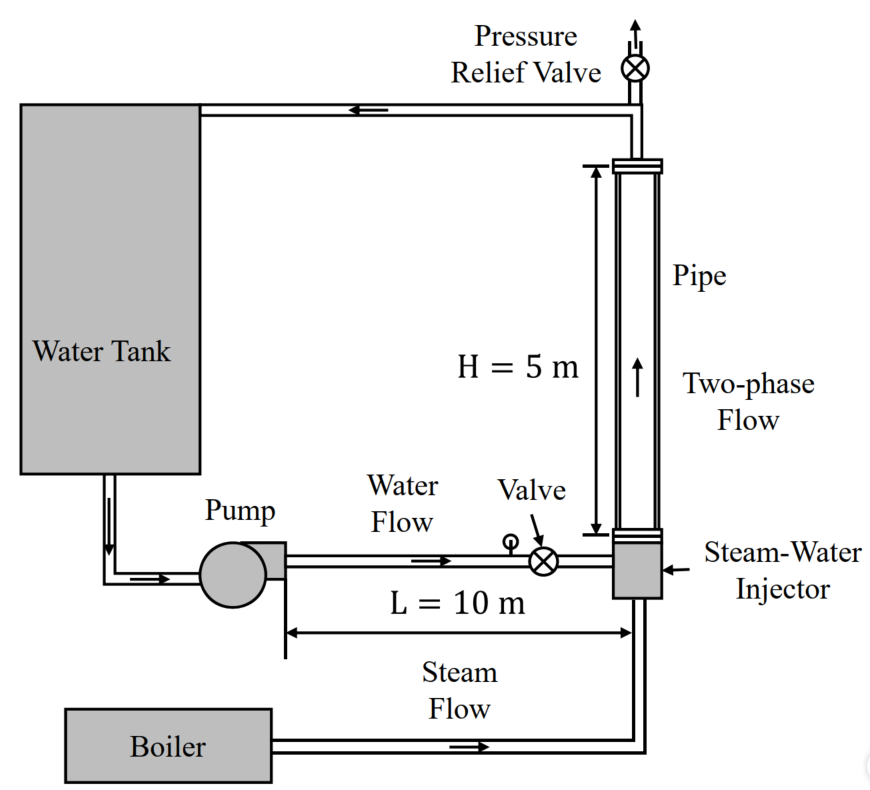
The figure shows the flow loop for the two-phase flow experiment in pipes. Water is driven by a pump and air is driven by an air compressor. They are mixed in the air-water injector, and then injected into the vertical pipe test section.

Assume that two phases flow in the vertical pipe with a diameter $\left(D_h\right)$ of $0.05\mathrm{m}$ at mass flux $(G)$ of $1000\mathrm{kg}/({\mathrm{m}}^2\cdot \mathrm{s})$ and void fraction $(⟨\alpha ⟩)$ of $0.75$ at the atmospheric condition. Calculate the hydrostatic pressure gradient. If the total height of the pipe section $(H)$ is $5\mathrm{m}$ , then what is the hydrostatic pressure loss? For simplicity, assume that the air and water fluid compressibility is negligible at the flow condition.

Assume that the void fraction change along the flow direction is negligible.

Fluid properties are given by:

$$\begin{array}{rl}& {\rho }_f=998\mathrm{kg}/{\mathrm{m}}^3,{\rho }_g=1.17\mathrm{kg}/{\mathrm{m}}^3\\ & {\mu }_f=1\times {10}^{-3}\mathrm{Pa}\cdot \mathrm{s},{\mu }_g=1.81\times {10}^{-5}\mathrm{Pa}\cdot \mathrm{s}\\ & g=9.8\mathrm{m}/{\mathrm{s}}^2\end{array}$$

Answer: The two-phase hydrostatic pressure gradient is given by:

$${\left(\frac{\mathrm{d}P}{\mathrm{d}x}\right)}_{\text{hydro}}={\rho }_{m}g=[⟨\alpha ⟩{\rho }_g+(1-⟨\alpha ⟩){\rho }_f]g.$$

If the pipe height is $5\mathrm{m}$, then:

$$\mathrm{\Delta }{P}_{\mathrm{hyd}}={\left(\frac{\mathrm{d}P}{\mathrm{d}x}\right)}_{\text{hydro}}H={\rho }_{m}gH=[⟨\alpha ⟩{\rho }_g+(1-⟨\alpha ⟩){\rho }_f]gH\approx 12268\mathrm{Pa}.$$

Q1-9

Following Question 4, calculate the two-phase frictional pressure gradient using the Lockhart-Martinelli method. What is the two-phase frictional pressure loss in the vertical pipe if the pipe length is $5\mathrm{m}$ ? The following friction factors can be used:

• Laminar flow:

$$f_{\text{fric }}=\frac{64}{\mathrm{R}\mathrm{e}}.$$

• Turbulent flow:

$$f_{\text{fric }}=\frac{0.316}{{\mathrm{R}\mathrm{e}}^{0.25}}$$

Two-phase multiplier is given by:

$${\mathrm{\Phi }}_f^2=1+\frac{C}{X}+\frac{1}{X^2}.$$

where

Liquid	Gas	C
Turbulent $({\mathrm{Re}}_f>2000)$	Turbulent $({\mathrm{Re}}_g>2000)$	20
Laminar $({\mathrm{Re}}_f<1000)$	Turbulent $({\mathrm{Re}}_g>2000)$	12
Turbulent $({\mathrm{Re}}_f>2000)$	Laminar $({\mathrm{Re}}_g<1000)$	10
Laminar $({\mathrm{Re}}_f<1000)$	Laminar $({\mathrm{Re}}_g<1000)$	5

The answer should be given using $\mathrm{Pa}$.

Answer: The relevant formulas:

$$\begin{array}{c}{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},2\mathrm{\Phi }}={\mathrm{\Phi }}_f^2{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},f},\text{ where }{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},f}=\frac{f}{D}\frac{{\rho }_f⟨j_f{⟩}^2}{2}\\ X=\sqrt{\frac{{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},f}}{{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},g}}}\text{(Lockhart-Martinelli coefficient)}\end{array}$$

The reynolds number about the liquid and gas are calculated by:

$$\begin{array}{rl}& {\mathrm{Re}}_f=\frac{{\rho }_f⟨j_f⟩D_h}{{\mu }_f}\approx 4.94\times {10}^4\\ & {\mathrm{Re}}_g=\frac{{\rho }_g⟨j_g⟩D_h}{{\mu }_g}\approx 3.44\times {10}^4\end{array}$$

Both gas and liquid flows are turbulent. Thus, liquid and gas friction factors are calculated by:

$$\begin{array}{rl}& f_{\mathrm{fric},f}=\frac{0.316}{{\mathrm{Re}}_f^{0.25}}\approx 0.0212\\ & f_{\mathrm{fric},g}=\frac{0.316}{{\mathrm{Re}}_g^{0.25}}\approx 0.0232\end{array}$$

Then, liuquid and gas pressure gradients are calculated by:

$$\begin{array}{rl}& {(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},f}=\frac{f_{\mathrm{fric},f}}{D_h}\frac{{\rho }_f⟨j_f{⟩}^2}{2}\approx 207\mathrm{Pa}/\mathrm{m}\\ & {(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},g}=\frac{f_{\mathrm{fric},g}}{D_h}\frac{{\rho }_g⟨j_g{⟩}^2}{2}\approx 30.7\mathrm{Pa}/\mathrm{m}.\end{array}$$

Then, the Lockhart-Martinelli coefficient is given by:

$$X=\sqrt{\frac{{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},f}}{{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},g}}}\approx 2.60.$$

$C=20$ for both gas and liquid are turbulent. The two-phase multiplier is calculated by:

$${\mathrm{\Phi }}_f^2=1+\frac{C}{X}+\frac{1}{X^2}\approx 8.85.$$

Eventually, we have

$$\begin{array}{rl}& {(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},2\mathrm{\Phi }}={\mathrm{\Phi }}_f^2{(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},f}\approx 1834\mathrm{Pa}/\mathrm{m}\\ ⟹& \mathrm{\Delta }{P}_{\mathrm{fric},2\mathrm{\Phi }}={(-\frac{\mathrm{d}P}{\mathrm{d}z})}_{\mathrm{fric},2\mathrm{\Phi }}H\approx 9168\mathrm{Pa}.\end{array}$$

Q1-10

Assume that pipes for transporting water has the diameter ($D$) of $0.1\mathrm{m}$. Calculate the liquid velocity in the water pipe if the liquid compressibility is negligible. What is the frictional pressure gradient in water pipe? If the water pipe has the length of $10\mathrm{m}$. what is the frictional pressure loss of water? The answer should be given using $\mathrm{Pa}$.

Answer:

According to Question 7, the liquid velocity in the pipe test section is:

$$⟨j_f⟩\approx 0.990\mathrm{m}/\mathrm{s}.$$

Then, the liquid volumetric flow rate is:

$$Q_f=\frac{⟨j_f⟩\pi D_h^2}{4}\approx 0.990\times \frac{\pi }{4}\times {0.05}^2=0.00194{\mathrm{m}}^3/\mathrm{s}.$$

Then, the liquid velocity in the water pipe is:

$$⟨j_{f,1\mathrm{\Phi }}⟩=\frac{4Q_f}{\pi D^2}\approx \frac{4\times 0.00194}{\pi \times {0.1}^2}=0.247\mathrm{m}/\mathrm{s}.$$

Then, the liquid single-phase Reynolds number is:

$${\mathrm{R}\mathrm{e}}_{f,1\mathrm{\Phi }}=\frac{{\rho }_f⟨j_{f,1\mathrm{\Phi }}⟩D}{{\mu }_f}\approx \frac{998\times 0.247\times 0.1}{1\times {10}^{-3}}\approx 24689.$$

The liquid single-phase flow is turbulent. Thus, the single-phase friction factor is:

$$f_{\mathrm{fric},1\mathrm{\Phi }}=\frac{0.316}{{\mathrm{R}\mathrm{e}}_{f,1\mathrm{\Phi }}^{0.25}}\approx \frac{0.316}{{24689}^{0.25}}=0.0252$$

Then, the liquid single-phase frictional pressure gradient is:

$$\begin{array}{rl}& {(-\frac{\mathrm{d}p}{\mathrm{d}x})}_{\mathrm{fric},1\mathrm{\Phi }}=\frac{f_{\mathrm{fric},1\mathrm{\Phi }}}{D}\frac{{\rho }_f⟨j_{f,1\mathrm{\Phi }}{⟩}^2}{2}\\ \approx & \frac{0.0252\times 998\times {0.247}^2}{0.1\times 2}\approx 7.70\mathrm{Pa}/\mathrm{m}\end{array}$$

Then, the liquid single-phase frictional pressure loss is:

$$\mathrm{\Delta }{P}_{\text{fric },1\mathrm{\Phi }}={(-\frac{\mathrm{d}p}{\mathrm{d}x})}_{\mathrm{fric},1\mathrm{\Phi }}L\approx 7.70\times 10\approx 77.0\mathrm{Pa}.$$

Q1-11

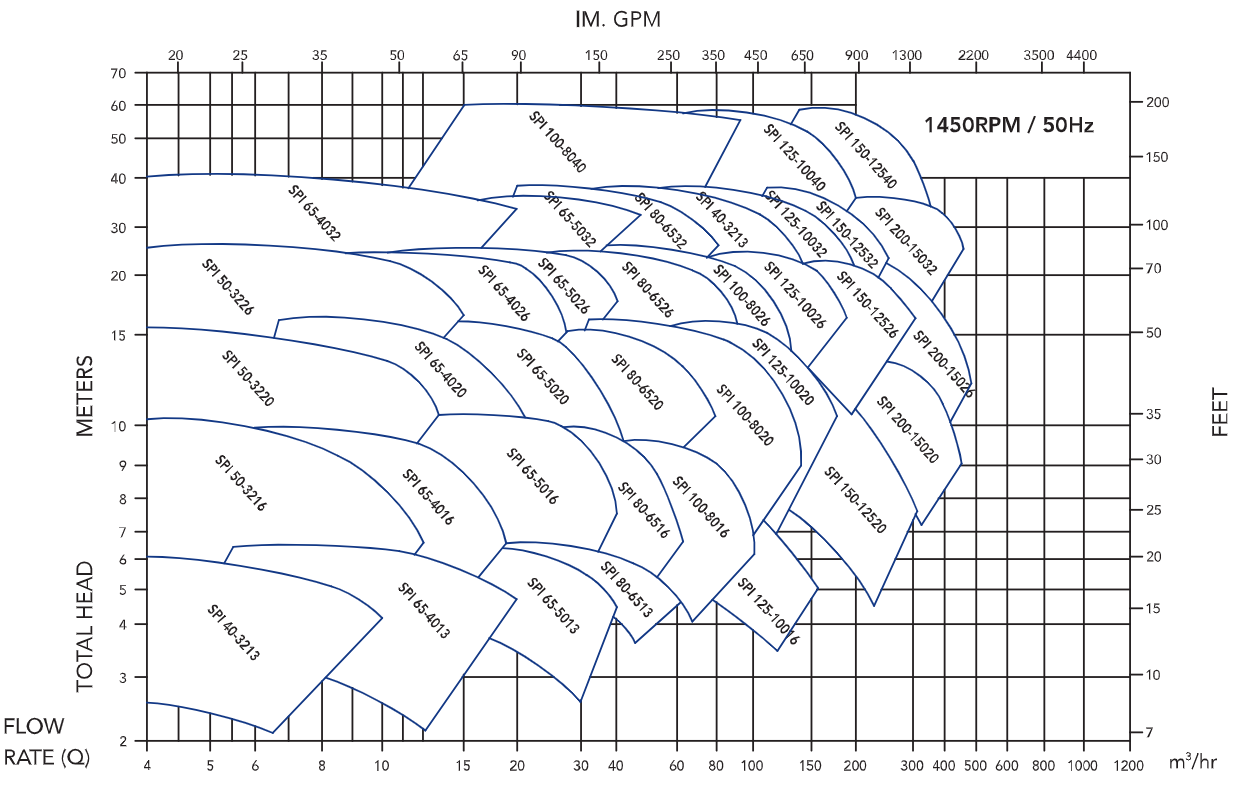> https://sppump.com/files/Superpower_In-Line_Pump_SPI_Series_.pdf#page=4.00

Assume that the total pressure loss from pump to the top of the test section consists of a pressure loss due to the horizontal single-phase liquid flow and a pressure loss due to the upward two-phase flow in the vertical test section. Use the values calculated in Questions 4 to 6 to obtain a total pressure loss. Then use the below chart to select a suitable pump. Hint: For pump selection, it is preferable to multiply the total estimated pressure loss by a factor $1.2$ can be used as a typical factor. The answer should be given using $\mathrm{Pa}$.

Answer:

The total pressure loss is equal to:

$$\begin{array}{rl}\mathrm{\Delta }{P}_{\text{total}}& =\mathrm{\Delta }{P}_{\text{fric},1\mathrm{\Phi }}+\mathrm{\Delta }{P}_{\text{fric},2\mathrm{\Phi }}+\mathrm{\Delta }{P}_{\text{hydro}}\\ & \approx 77.0+9168+12268\approx 21514\mathrm{Pa}\end{array}$$

Required head loss is equal to:

$$\mathrm{\Delta }{P}_{\text{pump}}=1.2\times \mathrm{\Delta }{P}_{\text{total}}\approx 25816\mathrm{Pa}\approx 2.64\mathrm{m}$$

pressure is converted to head (水头, height of liquid column in meters) using the formula $H=\mathrm{\Delta }P/{\rho }_{f}g$.

Required liquid flow rate is equal to:

$$Q_f=0.00194\frac{{\mathrm{m}}^3}{\mathrm{s}}=6.99\frac{{\mathrm{m}}^3}{\mathrm{hr}}$$

Thus, the SPI 40-3213 is selected.

Test2: heat transfer

Liquid water with the mass flux $(G)$ of $1000\mathrm{kg}/{\mathrm{m}}^2/\mathrm{s}$ is injected into a uniformly heated vertical pipe at pressure ( $P$ ) condition of $7.0\mathrm{MPa}$ and inlet temperature ( $T$ ) of ${250}^{\circ }\mathrm{C}$. The pipe has the diameter $\left(D_h\right)$ of $0.06\mathrm{m}$ and height of $10\mathrm{m}$ . It is heated by the heat source through the outside wall with a heat flux $\left(q_w^{\prime \prime }\right)$ of $5\times {10}^5\mathrm{W}/{\mathrm{m}}^2$.

• Mass flux: $G=1000\mathrm{kg}(m^2\cdot \mathrm{s})$
• Pressure condition: $P=7.0\mathrm{MPa}$
• Inlet temperature condition: $T_{\text{in}}={250}^{\circ }\mathrm{C}$
• Saturation temperature: $T_{\text{sat}}={286}^{\circ }\mathrm{C}$
• Diameter of the vertical pipe test section: $D_h=0.06\mathrm{m}$
• Height of the vertical pipe test section $H=10\mathrm{m}$
• Gravity acceleration: $g=9.8\mathrm{m}/{\mathrm{s}}^2$

Enthalpy of liquid water and steam:

• liquid enthalpy at inlet: $h_{\text{in }}=1086\mathrm{kJ}/\mathrm{kg}$
• Saturated liquid enthalpy: $h_{\text{sat},f}=1263\mathrm{kJ}/\mathrm{kg}$
• Saturated gas enthalpy: $h_{\text{sat},g}=2774\mathrm{kJ}/\mathrm{kg}$
• Latent heat: $h_{fg}=1511\mathrm{kJ}/\mathrm{kg}$

Properties of saturatod water and steam:

• Saturated liquid density: ${\rho }_f=741\mathrm{kg}/{\mathrm{m}}^3$
• Saturated liquid dynamic viscosity : ${\mu }_f=9.16\times {10}^{-5}\mathrm{Pa}\cdot \mathrm{s}$
• Saturated liquad thermal conductivity: $k_f=0.570\mathrm{W}/\mathrm{m}/\mathrm{K}$
• Saturated liquid isobaric heat capacity: $C_{pf}=5.38\mathrm{kJ}/\mathrm{kg}/\mathrm{K}$
• Saturated gas density: ${\rho }_g=36.5\mathrm{kg}/{\mathrm{m}}^3$.
• Saturated gas dynamic viscosity: ${\mu }_g=1.90\times {10}^{-5}\mathrm{Pa}$
• Steam-water surface tension $\sigma =0.0178\mathrm{N}/\mathrm{m}$
• Steel-water contact angles ${\varphi }_s={38}^{\circ }$

Typical boiling regime analysis

Step

1. Flow boundary conditions: liquid water injected, $G=1000\mathrm{kg}/({\mathrm{m}}^2\cdot \mathrm{s}),P=7.0\mathrm{MPa}$. Thermal boundary conditions: fixed heat flux or fixed wall temperature. Fluid system: steam-water.
2. Single-phase convection regime
3. Subcooled nucleate boiling regime
   • Onset of nucleate boiling (ONB)
   • Onset of significant void (OSV)
4. Saturated boiling regime
   • Convective boiling heat transfer
   • Nucleate boiling heat transfer
5. Critical heat flux

Assumptions

• Ignore the pressure loss in two-phase mixing section
• Air and water fluid compressibility is negligible.
• Water properties change with temperature is negligible.

Q2-1

Assume that water properties do not vary significantly in single－phase flow section，what are the Reynolds number and Prandtl number for liquid water using the average properties of under－saturated water？Calculate the Nussel nermber and liquid convective heat transfer coefficient using the Dittus－Boelet equation

$$\begin{array}{c}{\mathrm{N}\mathrm{u}}_f=0.023{\mathrm{R}\mathrm{e}}_f^{0.8}{\mathrm{P}\mathrm{r}}_f^{0.4}\\ {\mathrm{R}\mathrm{e}}_f=\frac{G{D}_h}{{\mu }_f}\\ {\mathrm{P}\mathrm{r}}_f=\frac{C_{pf}{\mu }_f}{k_f}\\ {\mathrm{N}\mathrm{u}}_f=\frac{h_f{D}_h}{k_f}\end{array}$$

Answer: Liquid Reynolds number

$${\mathrm{R}\mathrm{e}}_f=\frac{G{D}_h}{{\mu }_f}=\frac{1000\times 0.06}{9.16\times {10}^{-5}}\approx 6.55\times {10}^5.$$

Liquid Prandtl number

$${\mathrm{Pr}}_f=\frac{C_{pf}{\mu }_f}{k_f}=\frac{5.38\times {10}^3\times 9.16\times {10}^{-5}}{0.570}\approx 0.865.$$

Liquid Nusselt number

$${\mathrm{N}\mathrm{u}}_f=0.023{\mathrm{R}\mathrm{e}}_f^{0.8}{\mathrm{P}\mathrm{r}}_f^{0.4}\approx 976.$$

Liquid convective heat transfer coefficient

$$h_f=\frac{{\mathrm{N}\mathrm{u}}_f{k}_f}{D_h}=9272\mathrm{W}/{\mathrm{m}}^2/\mathrm{K}$$

Q2-2

What is the temperature difference between the wall temperature and mean bulk liquid temperature (wall super heat [${}^{\circ }\mathrm{C}$])?

$$q_w^{″}=h\mathrm{\Delta }T.$$

Answer: The temperature difference between the wall and the fluid is calculated by the heat flux:

$$q^{″}=h_f\mathrm{\Delta }T⟹\mathrm{\Delta }T=\frac{q_w^{″}}{h_f}\approx \frac{5\times {10}^5}{9272}{}^{\circ }\mathrm{C}\approx {53.9}^{\circ }\mathrm{C}.$$

Q2-3

Determine the temperature for the onset of nucleate boiling, $T_{\text{ONB}}$, using Basu et al. (2004) correlation

$$\mathrm{\Delta }{T}_{\text{ONB}}=\frac{\sqrt{2}}{F\left({\varphi }_S\right)}{\left(\frac{\sigma T_{\text{sat}}{q}_w^{″}}{{\rho }_g{h}_{fg}{k}_f}\right)}^{0.5}$$

where

$$\begin{array}{c}F\left({\varphi }_s\right)=1-\exp [-{\left(\frac{\pi {\varphi }_s}{180}\right)}^3-0.5\left(\frac{\pi {\varphi }_s}{180}\right)]\\ {\varphi }_{\mathrm{s}}={38}^{\circ }.\end{array}$$

Answer:

Contact angle, ${\varphi }_s={38}^{\circ }$, thus:

$$F({\varphi }_S={38}^{\circ })=1-\exp [-{\left(\frac{\pi \times 38}{180}\right)}^3-0.5\left(\frac{\pi \times 38}{180}\right)]\approx 0.464.$$

Then:

$$\begin{array}{rl}\mathrm{\Delta }{T}_{\text{ONB}}& =\frac{\sqrt{2}}{F\left({\varphi }_S\right)}{\left(\frac{\sigma T_{\text{sat}}{q}_w^{″}}{{\rho }_g{h}_{fg}{k}_f}\right)}^{0.5}\\ & \approx \frac{\sqrt{2}}{0.464}{\left(\frac{0.0178\times 559.15\times 5\times {10}^5}{36.5\times 1511000\times 0.570}\right)}^{0.5}\approx {1.21}^{\circ }\mathrm{C}\end{array}$$

Therefore

$$T_{ONB}=\mathrm{\Delta }{T}_{ONB}+T_{sat}\approx 1.21+559\mathrm{K}=560\mathrm{K}\approx {287}^{\circ }\mathrm{C}$$

Q2-4

Calculate the temperature and length for the onset of significant void, $T_{ONB}$

$$\begin{array}{rl}& \mathrm{P}\mathrm{e}=\frac{G{D}_h{C}_{pf}}{k_f}\\ \text{For }& \mathrm{P}\mathrm{e}<7\times {10}^4:\\ & T_{\text{sat }}-T_D=0.0022\left(\frac{q_w^{″}{D}_h}{R_f}\right)\\ \text{For }& \mathrm{P}\mathrm{e}>7\times {10}^4:\\ & T_{\text{sat }}-T_D=154\left(\frac{q_w^{″}}{G{C}_{pf}}\right)\\ & Z_D=\frac{\frac{\pi D_h^2}{4}G{C}_{pf}(T_D-T_{in})}{\pi D_h{q}^{″}}.\end{array}$$

Answer:

$$\begin{array}{c}\mathrm{Pe}=\frac{1000\times 0.06\times 5380}{0.570}\approx 5.66\times {10}^5>7\times {10}^4:\\ T_{\text{sat}}-T_D=154\left(\frac{5\times {10}^5}{1000\times 5380}\right)\approx {14.3}^{\circ }\mathrm{C}.\end{array}$$

Hence:

$$T_{\mathrm{D}}\approx T_{\text{sat}}-14.3\approx 559-14.3\approx 545\mathrm{K}\approx {272}^{\circ }\mathrm{C}.$$

Using energy balance equation:

$$\begin{array}{rl}{Z}_D& =\frac{\frac{\pi D_h^2}{4}G{C}_{pf}(T_D-T_{\text{in}})}{\pi D_h{q}^{″}}\\ & \approx \frac{0.06\times 1000\times 5380\times (545-523)}{4\times 5\times {10}^5}\approx 3.50\mathrm{m}.\end{array}$$

Q2-5

In another scenario, assume that the heat flux is unknown and the wall temperature is fixed at ${326}^{\circ }\mathrm{C}$. Chen's correlation is used to calculate two-phase heat transfer coefficient and heat flux at $x=0.1$. Saturation pressure at ${326}^{\circ }\mathrm{C}$ is $12.2\mathrm{MPa}$ .

$$\begin{array}{rl}& q^{″}=h_{2\mathrm{\Phi }}(T_w-T_{\text{sat}}),h_{2\mathrm{\Phi }}=h_{\text{NB}}+h_c\\ & h_c=0.023{\mathrm{Re}}_f^{0.8}{\mathrm{Pr}}_f^{0.4}\frac{k_f}{D_h}F\\ & h_{\text{NB}}=S\times 0.00122\left[\frac{{\left(k^{0.79}{C}_p^{0.45}{\rho }^{0.49}\right)}_f}{{\sigma }^{0.5}{\mu }_f^{0.29}{h}_{fg}^{0.24}{\rho }_g^{0.24}}\right]\mathrm{\Delta }{T}_{\mathrm{s}\mathrm{a}\mathrm{t}}^{0.24}\mathrm{\Delta }{P}^{0.75}\end{array}$$

where

$$\begin{array}{rl}& S=\frac{1}{1+2.53\times {10}^{-6}{\mathrm{R}\mathrm{e}}^{1.17}}\\ & \mathrm{R}\mathrm{e}={\mathrm{R}\mathrm{e}}_f{F}^{1.25}\\ & {\mathrm{R}\mathrm{e}}_f=\frac{G(1-x)D_h}{{\mu }_f}\\ & F=\{\begin{array}{rlrl}& 1& & \text{for }\frac{1}{X_{tt}}<0.1\\ & 2.35{(0.213+\frac{1}{X_{tt}})}^{0.736}& & \text{for }\frac{1}{X_{tt}}>0.1\end{array}\\ & X_{tt}={\left(\frac{1-x}{x}\right)}^{0.9}{\left(\frac{{\rho }_g}{{\rho }_f}\right)}^{0.5}{\left(\frac{{\mu }_f}{{\mu }_g}\right)}^{0.1}\\ & \mathrm{\Delta }{T}_{\mathrm{s}\mathrm{a}\mathrm{t}}=T_w-T_{\mathrm{s}\mathrm{a}\mathrm{t}}\\ & \mathrm{\Delta }P=P\left(T_w\right)-P\left(T_{\mathrm{s}\mathrm{a}\mathrm{t}}\right)\end{array}$$

The answer of $h_{\text{NB}}$ should be given in $\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right)$.

Answer:

$$\begin{array}{rl}{\mathrm{Re}}_f=& \frac{G(1-x)D_h}{{\mu }_f}=\frac{1000(1-0.1)\times 0.06}{9.16\times {10}^{-5}}=5.90\times {10}^5\\ {\mathrm{Pr}}_f=& \frac{{\mu }_f{C}_{pf}}{k_f}=\frac{9.16\times {10}^{-5}\times 5380}{0.570}=0.865\\ X_{tt}=& {\left(\frac{1-x}{x}\right)}^{0.9}{\left(\frac{{\rho }_g}{{\rho }_f}\right)}^{0.5}{\left(\frac{{\mu }_f}{{\mu }_g}\right)}^{0.1}\\ =& {\left(\frac{1-0.1}{0.1}\right)}^{0.9}{\left(\frac{36.5}{741}\right)}^{0.5}{\left(\frac{9.16\times {10}^{-5}}{1.9\times {10}^{-5}}\right)}^{0.1}\approx 1.88.\end{array}$$

Since $\frac{1}{X_{tt}}\approx 0.533>0.1$,

$$\begin{array}{rl}F& =2.35{(0.213+\frac{1}{X_{\mathrm{tt}}})}^{0.736}\approx 1.89\\ h_c& =0.023{\mathrm{Re}}_f^{0.8}{\mathrm{Pr}}_f^{0.4}\frac{k_f}{D_h}F\\ & \approx 0.023{(5.90\times {10}^5)}^{0.8}(0.865{)}^{0.4}\left(\frac{0.570}{0.06}\right)1.89\\ & \approx 1.61\times {10}^4\mathrm{W}/\left({\mathrm{m}}^2\mathrm{K}\right)\end{array}$$

On the other hand:

$$\begin{array}{rl}& \mathrm{\Delta }{T}_{\mathrm{s}\mathrm{a}\mathrm{t}}=T_w-T_{\mathrm{s}\mathrm{a}\mathrm{t}}=(326-286{)}^{\circ }\mathrm{C}={40}^{\circ }\mathrm{C}\\ & \mathrm{\Delta }P=P\left(T_w\right)-P(T_{\mathrm{s}\mathrm{a}\mathrm{t}})=(12.2-7)\mathrm{MPa}=5.2\times {10}^6\mathrm{Pa}\\ ⟹& \mathrm{Re}={\mathrm{Re}}_f{F}^{1.25}\approx 1.31\times {10}^6\\ ⟹& S=\frac{1}{1+2.53\times {10}^{-6}{\mathrm{R}\mathrm{e}}^{1.17}}\approx 0.0268\\ ⟹& h_{NB}=S\times 0.00122\left[\frac{{\left(k^{0.79}{C}_p^{0.45}{\rho }^{0.49}\right)}_f}{{\sigma }^{0.5}{\mu }_f^{0.29}{h}_{fg}^{0.24}{\rho }_g^{0.24}}\right]\mathrm{\Delta }{T}_{\mathrm{s}\mathrm{a}\mathrm{t}}^{0.24}\mathrm{\Delta }{P}^{0.75}\approx 1.04\times {10}^4\mathrm{W}/({\mathrm{m}}^2\cdot \mathrm{K}).\end{array}$$

Thus,

$$\begin{array}{rl}& h_{2\mathrm{\Phi }}=h_{\text{NB}}+h_c\approx 2.65\times {10}^4\mathrm{W}/({\mathrm{m}}^2\cdot \mathrm{K})\\ ⟹& q^{″}=h_{2\mathrm{\Phi }}(T_w-T_{\text{sat}})\approx 1.06\times {10}^6\mathrm{W}/{\mathrm{m}}^2.\end{array}$$

Q2-6

Assume that the liquid velocity is zero (pool conditions), calculate the critical heat flux using Zuber's correlation:

$$q_{\text{cr}}^{\prime \prime }={\rho }_g{j}_g{h}_{fg}$$

where the vapor velocity leading to the onset of fluidization $j_g$ is given by:

$$j_g=0.13{\left[\frac{\sigma ({\rho }_f-{\rho }_g)g}{{\rho }_g^2}\right]}^{1/4}$$

The answer of $q_{\text{cr}}^{\prime \prime }$ should be given in $\mathrm{W}/{\mathrm{m}}^2$.

Answer:

$$\begin{array}{rl}& j_g=0.13{\left[\frac{\sigma ({\rho }_f-{\rho }_g)g}{{\rho }_g^2}\right]}^{1/4}\approx 0.0176\mathrm{m}/\mathrm{s}\\ ⟹& q_{\text{cr}}^{\prime \prime }={\rho }_g{j}_g{h}_{fg}\approx 3.95\times {10}^6\mathrm{W}/{\mathrm{m}}^2.\end{array}$$