Two-Phase Heat Transfer

Nucleation superheat

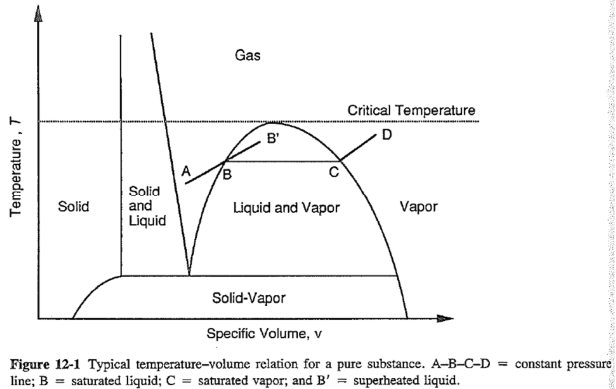
Phase change: liquid -> gas / gas -> liquid

• Homogeneous nucleation 均匀成核 (A-B')
• Heterogeneous nucleation 异相成核 (A-B-C-D)

Specific volume = density${}^{-1}$

Clausius-Clapeyron relation

Mechanical equilibrium:

$$(p_b-p_l)\pi r^{\ast 2}=\sigma 2\pi r^{\ast }\text{ or }\mathrm{\Delta }p=p_b-p_l=\frac{2\sigma }{r^{\ast }}$$

• $p_b$: Internal pressure in bubble
• $p_l$: Pressure outside the bubble
• $r^{\ast }$: radius of bubble
• $\sigma$: coefficient of surface tension 表面张力

[core] Clausius-Clapeyron relation b/w $p_{\mathrm{sat}}$ & $T_{\mathrm{sat}}$ (where $h_{\mathrm{fg}}$ is Latent heat of phase change 相变潜热 / enthalpy of vaporization):

The Clausius-Clapeyron equation specifies the temperature dependencies of pressure, most importantly, vapor pressure, at a discontinuous phase transition b/w two phase of matter of a single contituent

$$\begin{array}{rl}& {\left(\frac{\mathrm{d}p}{\mathrm{d}T}\right)}_{\text{sat }}=\frac{h_{\mathrm{fg}}}{T_{\text{sat }}({\nu }_{\mathrm{g}}-{\nu }_{\mathrm{f}})}\\ \underset{{\nu }_{\mathrm{g}}\gg {\nu }_{\mathrm{f}}}{\overset{\text{ Saturated vapor }}{\to }}& \frac{\mathrm{d}{p}_{\mathrm{g}}}{\mathrm{d}{T}_{\mathrm{g}}}=\frac{h_{\mathrm{fg}}}{T_{\mathrm{g}}\left({\nu }_{\mathrm{g}}\right)}\stackrel{p_{\mathrm{g}}{\nu }_{\mathrm{g}}=R{T}_{\mathrm{g}}}{\to }\frac{\mathrm{d}{p}_{\mathrm{g}}}{p_{\mathrm{g}}}=\frac{h_{\mathrm{fg}}}{R{T}_{\mathrm{g}}^2}\mathrm{d}{T}_{\mathrm{g}}\\ & \ln \left(\frac{p_{\mathrm{b}}}{p_l}\right)=-\frac{h_{\mathrm{fg}}}{R}(\frac{1}{T_{\mathrm{b}}}-\frac{1}{T_{\text{sat }}})\\ & T_{\mathrm{b}}-T_{\text{sat }}=\frac{R{T}_{\mathrm{b}}{T}_{\text{sat }}}{h_{\mathrm{fg}}}\ln \left(\frac{p_{\mathrm{b}}}{p_l}\right)\\ \underset{T_{\text{sat }}:\text{ Saturation temperature at }{p}_{\mathrm{l}}}{\overset{T_{\mathrm{b}}:\text{ Saturation temperature at }{p}_{\mathrm{b}}}{\to }}& T_{\mathrm{b}}-T_{\text{sat }}=\frac{R{T}_{\mathrm{b}}{T}_{\text{sat }}}{h_{\mathrm{fg}}}\ln (1+\frac{2\sigma }{p_l{r}^{\ast }})\end{array}$$

Superheat ($=T_{\mathrm{b}}-T_{\text{sat }}$ ) required to maintain a bubble

when $2\sigma /p_l{r}^{\ast }\ll 1,p_{\mathrm{b}}\simeq p_l.R{T}_{\mathrm{b}}/p_{\mathrm{b}}={\nu }_{\mathrm{b}}\simeq {\nu }_{\mathrm{fg}}$ .

$$T_{\mathrm{b}}-T_{\text{sat }}\simeq \frac{R{T}_{\mathrm{b}}{T}_{\mathrm{sat}}2\sigma }{h_{\mathrm{fg}}{p}_{\mathrm{b}}{r}^{\ast }}\simeq \frac{2\sigma T_{\text{sat }}{\nu }_{\mathrm{fg}}}{h_{\mathrm{fg}}}\left(\frac{1}{r^{\ast }}\right)p_l\ll p_{\mathrm{c}}$$

where $p_c$ is Critical pressure.

Superheat for homogeneous nucleation of water at $p=0.1\mathrm{MPa}:{220}^{\circ }\mathrm{C}$

Heterogeneous nucleation: dissolved gas & microcavities at surface

Pool boiling

• Boiling curve: Heat-transfer regime of pool boiling
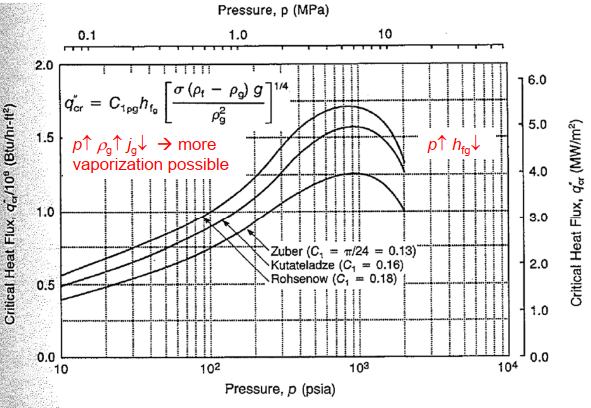
• Critical heat flux: Linked with onset of pool fluidization (suspension of liquid by vapor stream)

Hydrodynamic instability:

• Kelvin- Helmholtz instability: 2 fluid flow counterpart: critical heat flux =...

$$q_{\mathrm{cr}}^{\prime \prime }={\rho }_g{h}_{\mathrm{fg}}{j}_g=C_1{\rho }_g{h}_{\mathrm{fg}}{\left[\frac{\sigma ({\rho }_f-{\rho }_g)g}{{\rho }_g^2}\right]}^{1/4}$$

where $C_1=0.13$.

Flow boiling

• Heat transfer regime: Mass flow rate, fluids, geometry, heat flux magnitude and distribution
• Dry-out type CHF: High quality
• DNB (departure from nucleate boiling) type CHF (similar to CHF in pool boiling): Low quality

Enthalpy 焓 [$\mathrm{J}/\mathrm{kg}$] at $z$ from inlet:

$$h=h_{l,in}+\frac{4q_w^{″}z}{DG}$$

$\frac{4q_w^{″}z}{DG}$ comes from

1. The area of pipe wall: $z\pi D$
2. The whole heat: $\mathrm{\Delta }Q=q_w^{″}\cdot z\pi D$
3. The enthalpy increase: $\mathrm{\Delta }Q/W=\mathrm{\Delta }Q/(G\cdot \pi D^2/4)=\frac{4q_w^{″}z}{DG}$

Thermal equilibrium quality at $z$ from inlet:

$$x_{eq}=\frac{h-h_{l,\mathrm{sat}}}{h_{fg}}=\frac{h_{l,in}+\frac{4q_w^{″}z}{DG}-h_{l,\mathrm{sat}}}{h_{fg}}$$

• $h_{l,\mathrm{sat}}$: Saturated enthalpy
• When $h=h_{fg}+h_{l,\mathrm{sat}},x_{eq}=1$

For boiling curve:

• single-phase flow: $q^{″}=h(T_w-T_{\mathrm{sat}})$
• The corner: $(T_w-T_{\mathrm{sat}}{)}^{m-1}$
• 2-phase flow: $q^{″}=h(T_w-T_{\mathrm{sat}}{)}^m,m\simeq 3$

Subcooled boiling

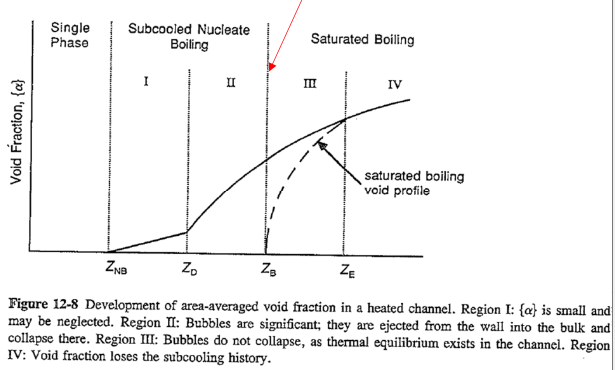
1. Region I: Subcooled nucleate boiling (Onset of nucleate boiling, $Z_{\mathrm{NB}}$: mean or bulk temperature below Tsat)
2. Region II: Subcooled nucleate boiling (Onset of significant void, $Z_{\mathrm{D}}$)
3. Region III: Saturated boiling ($x_{eq}=0$: since liquid does not reach saturation condition due to the bubble presence and non-equilibrium)
4. Region IV: Saturated boiling (thermal equilibrium condition at $Z_{\mathrm{E}}$)

• For $Z_{\mathrm{D}}$, that's Saha-Zuber correlation to determine
• For the curve: profile-fit method

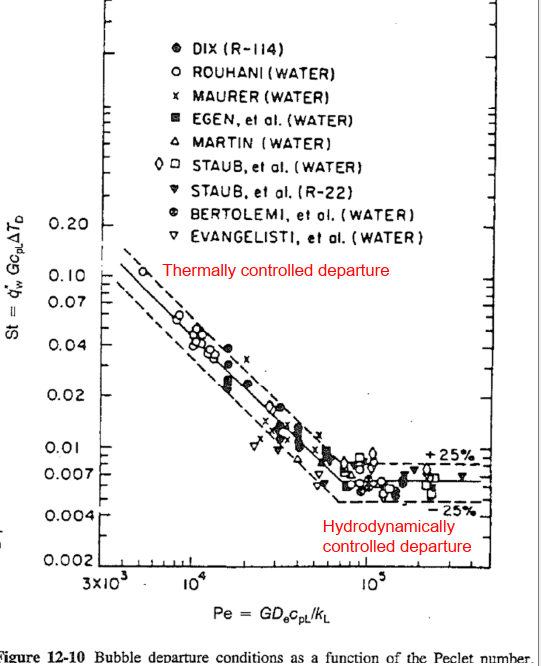
Net vapor generation (Bubble departure)

Net vapor generation: The point at which bubbles can depart from the wall before they suffer condensation ($Z_{\mathrm{D}}$)

在流体中，蒸汽的“产生”速度开始大于“凝结”速度，从而出现净增的蒸汽

• Thermally controlled departure: The wall heat flux is balanced by heat removal due to liquid subcooling at $Z_{\mathrm{D}}$.
• Hydrodynamically controlled departure: The bubble detachment is primarily the result of drag (or shear) force overcoming the surface tension force

Saha-Zuber correlation: (empirical) $\mathrm{St}=\frac{\mathrm{Nu}}{\mathrm{Re}\mathrm{Pr}}\sim \mathrm{Pe}=\frac{\mathrm{Nu}}{\mathrm{St}}=\frac{G{D}_n{c}_{pf}}{k_f}$

$$x_{eq}(Z_D)=\{\begin{array}{ll}-0.0022\frac{q^{″}{D}_n{c}_{pf}}{k_f{h}_{fg}}& \mathrm{Pe}\le 70000\\ -153.85\frac{q^{″}}{G{h}_{fg}}& \mathrm{Pe}\ge 70000\end{array}$$

For temperature:

$$T_{\mathrm{sat}}-T_{\mathrm{bulk}}=\{\begin{array}{ll}0.0022\frac{q^{″}{D}_n}{k_f}& \mathrm{Pe}\le 70000\\ 153.85\frac{q^{″}}{G{c}_{pl}}& \mathrm{Pe}\ge 70000\end{array}$$

Subcooled flow quality and void fraction

Profile-fit approach: Currently accepted approach for determining the flow quality in subcooled region

$$x(z)=x_{eq}(z)-x_{eq}(Z_{\mathrm{D}})\exp [\frac{x_{eq}(z)}{x_{eq}(Z_{\mathrm{D}})}-1]$$

The flow quality $x(z)$:

• $=0$ at $Z_{\mathrm{D}}$
• approaches $x_{eq}(z)$ asymptotically as $z$ increases
• When $x_{eq}(z)=0,x(z)=-\frac{1}{e}{x}_{eq}(Z_D)\approx -0.368x_{eq}(Z_D)$

For quality:

$$x\ne x_{eq}$$

• well-saturated boiling flow:

$$x\approx x_{eq}$$

• Subcooled boiling flow:

$$x\ge 0,x_{eq}<0$$

Using profile-fit approach to obtain $x_{eq}$ How to determine $Z_{\mathrm{D}}$: Profile-fit method

pump $\to$

• Bernoulli's Equation
  • Major loss
  • Minor loss

Mission: prediction of void fraction for heat transfer, etc.

1. To predict the void fraction $⟨\alpha ⟩$, the Drift-flux model is used (need $⟨x⟩$)

Drift-flux model:

$$⟨\alpha ⟩=\frac{⟨j_g⟩}{C_0(⟨j_g⟩+⟨j_f⟩)+⟨⟨v_{fg}⟩⟩}$$

where

$$⟨j_g⟩=\frac{G⟨x_f⟩}{{\rho }_g},⟨j_f⟩=\frac{G(1-⟨x_f⟩)}{{\rho }_f}$$

and $x_f$ is the flow quality

• For HEM, $⟨\alpha ⟩=⟨j_g⟩/(⟨j_g⟩+⟨j_f⟩)$ and 20% overprediction

2. Distribution parameter $C_0$ and drift velocity $⟨⟨v_{fg}⟩⟩$ can be obtained by formulas in the last chapter
3. To obtain the flow quality $⟨x_f⟩$, Profile-fit approach ($x_f\sim x_{eq}$) and OSV model (onset of significant void) are used $(\text{need }{x}_{eq}(z),x_{eq}(Z_D))$
   1. To obtain $x_{eq}$, Thermal equilibrium quality is used
   2. To obtain $x_{eq}(Z_D)$, the Saha-Zuber correlation is used

Saturated Cooling

Heat transfer:

• $1\varphi :q^{″}=h_{1\varphi }(T_w-T_{\mathrm{bulk}})$
  • $\mathrm{Nu}=\frac{h_{1\varphi }D}{k_f}$ where $k_f$ is the thermal conductivity
  • Dittus-Boelton equation for $1\varphi$ convective heat transfer (Turbulent flow):$$\mathrm{Nu}=0.023{\mathrm{Re}}^{0.8}{\mathrm{Pr}}^m,m=0.3(\text{cooling}),0.4(\text{heating})$$
  • $\mathrm{Re}={\rho }_f{j}_{f}D/{\mu }_f$ where $j_f=G(1-x)/{\rho }_f$
• $2\varphi :q^{″}=h_{2\varphi }(T_w-T_{\mathrm{sat}})$ (Saturated boiling flow)
  • $h_{2\varphi }=\underset{\text{nucleate boiling}}{\underbrace{h_{\mathrm{NB}}}}+\underset{\text{forced convective flow}}{\underbrace{h_C}}(\text{Chen correlation})$

Boling incipience

Fourier's law:

$$q^{″}=-k_l\frac{\partial T}{\partial r}\sim k_l\frac{T_b-T_{\mathrm{sat}}}{r^{\ast }}$$

Clausius-Clapeyron relation:

$$T_w=T_{\mathrm{sat}}+\frac{2\sigma T_{\mathrm{sat}}{v}_{fg}}{h_{fg}}\frac{1}{r^{\ast }}.$$

Thus

$$q^{″}=\frac{k_l{h}_{fg}}{8\sigma T_{\mathrm{sat}{v}_{fg}}}(T_w-T_{\mathrm{sat}}{)}^2.$$

Quiz3

Water is injected with a velocity of $1.5\mathrm{m}/\mathrm{s}$ into a uniformly heated vertical pipe with a diameter of $0.05\mathrm{m}$ and length of $10\mathrm{m}$ receiving a heat flux of $5\times {10}^6\mathrm{W}/{\mathrm{m}}^2$. Inlet pressure and temperature of water are $4.64\mathrm{MPa}$ and ${25}^{\circ }\mathrm{C}$. Saturation temperature, $T_{\mathrm{sat}}$, at $4.64\mathrm{MPa}$ is ${259}^{\circ }\mathrm{C}$. Saturated liquid enthalpy, $h_{l,sat}$, and enthalpy of vaporization, $h_{fg}$, are $1132\mathrm{kJ}/\mathrm{kg}$ and $1665\mathrm{kJ}/\mathrm{kg}$. Saturated liquid density and saturated steam density are $785\mathrm{kg}/{\mathrm{m}}^3$ and $23.4\mathrm{kg}/{\mathrm{m}}^3$. Enthalpy of water at $4.64\mathrm{MPa}$ and ${25}^{\circ }\mathrm{C}$ is $123\mathrm{kJ}/\mathrm{kg}$. Density of the saturated liquid can be used as a good estimation of density of subcooled water. Other average fluid properties are $C_{pl}=4980\mathrm{J}/\mathrm{kg}\cdot K,k_l=0.570\mathrm{W}/\mathrm{m}\cdot K$, ${\mu }_l=9.4\times {10}^{-5}\mathrm{kg}/(m\cdot \mathrm{s})$. Surface tension at the saturation pressure can be used approximately for the calculation $(\sigma =0.0329\mathrm{N}/\mathrm{m})$.

1. Calculate the mixture mass flux (unit in $\mathrm{kg}/{\mathrm{m}}^2\mathrm{s}$). In thr uniformly heated pipe:

$$G={\rho }_f{v}_f=785\times 1.5\mathrm{kg}/{\mathrm{m}}^2\mathrm{s}=1177.5\mathrm{kg}/{\mathrm{m}}^2\mathrm{s}.$$

2. Calculate the enthalpy at $4\mathrm{m}$ from the pipe inlet (unit in $\mathrm{kJ}/\mathrm{kg}$).

$$h=h_{l,in}+\frac{4q_w^{″}z}{DG}=(123+\frac{4\times 5\times {10}^3\times 4}{0.05\times 1177.5})\mathrm{kJ}/\mathrm{kg}\approx 1481.811\mathrm{kJ}/\mathrm{kg}.$$

3. Calculate the thermal equilibrium quality located at the $4\mathrm{m}$ from the pipe inlet. Thermal equilibrium quality is calculated as

$$x_e(z){|}_{z=4}=\frac{h(z){|}_{z=4}-h_{l,\mathrm{sat}}}{h_{fg}}=\frac{1481.811-1132}{1665}\approx 0.210.$$

4. Calculate the Peclet number for the inlet liquid.

$$\mathrm{Pe}=\frac{G{C}_{pl}D}{k_l}=\frac{1177.5\times 4980\times 0.05}{0.570}\approx 5.143816\times {10}^5$$

5. Calculate the temperature for onset of significant void, $T_D$, (unit in $\mathrm{K}$). According to Saha-Zuber correlation, when $\mathrm{Pe}>70000$:

$$T_{\mathrm{sat}}-T_D=153.85\frac{q^{″}}{G{C}_{pl}}=153.85\times \frac{5\times {10}^6}{1177.5\times 4980}\mathrm{K}\approx 131.183\mathrm{K}$$

Thus $T_D\approx T_{\mathrm{sat}}-131.3\mathrm{K}\approx (259+273.15-131.183)\mathrm{K}\approx 400.967\mathrm{K}$

6. Calculate the length at which onset of significant void occurs, $Z_D$, (unit in $\mathrm{m}$).

$$Z_D=\frac{\frac{\pi D_h^2}{4}G{C}_{pl}(T_D-T_{in})}{\pi D_h{q}_w^{\prime \prime }}=\frac{D_{h}G{C}_{pl}(T_D-T_{in})}{4q_w^{\prime \prime }}\approx 1.507\mathrm{m}.$$

7. Calculate the equilibrium quality at $Z_D,x_e(Z_D)$.

Based on Saha-Zuber correlation, when $\mathrm{Pe}>70000$: (Not right while using this formula)

$$x_e(Z_D)=-153.85\frac{q^{″}}{G{h}_{fg}}=-153.85\times \frac{5\times {10}^6}{1177.5\times 1665\times {10}^3}\approx -0.392.$$

$$\begin{array}{c}h{|}_{z=Z_D}=h_{l,in}+\frac{4q_w^{″}{Z}_D}{DG}\approx (123+\frac{4\times 5\times {10}^3\times 1.507}{0.05\times 1177.5})\mathrm{kJ}/\mathrm{kg}\approx 634.392\mathrm{kJ}/\mathrm{kg}\\ x_e(Z_D)=\frac{h{|}_{z=Z_D}-h_{l,\text{sat}}}{h_{fg}}\approx -0.299.\end{array}$$

8. Calculate the quality at $Z=2\mathrm{m},x(Z=2\mathrm{m})$. The quality is calculated based on the profile-fit approach:

$$x(z){|}_{z=2\mathrm{m}}=x_e(z){|}_{z=2\mathrm{m}}-x_e(Z_{\mathrm{D}})\exp [\frac{x_e(z){|}_{z=2\mathrm{m}}}{x_e(Z_{\mathrm{D}})}-1]$$

where

$$x_e(z){|}_{z=2\mathrm{m}}=\frac{h_{l,\mathrm{in}}+\frac{4q^{″}z{|}_{z=2\mathrm{m}}}{GD}-h_{l,\mathrm{sat}}}{h_{fg}}\approx -0.198$$

Thus ::: details(Wrong answer in 7th leads to wrong answer here)

$$x(z){|}_{z=2\mathrm{m}}\approx -0.198-(-0.392)\times \exp [\frac{-0.198}{-0.392}-1]\approx 0.0411$$

:::

$$x(z){|}_{z=2\mathrm{m}}\approx -0.198-(-0.299)\times \exp [\frac{-0.198}{-0.299}-1]\approx 0.0153.$$

9. Calculate the distribution parameter, $C_0$, at $Z=2\mathrm{m}$. Given:

$$\begin{array}{rl}& C_0=\beta [1+(1/\beta -1{)}^b]\\ & b=({\rho }_g/{\rho }_f{)}^{0.1}\\ & \beta =(x/{\rho }_g)/(x/{\rho }_g+(1-x)/{\rho }_f)\end{array}$$

According to the given formula:

Wrong answer

$$\begin{array}{rl}& \beta \approx \frac{0.0411}{23.4}/(\frac{0.0411}{23.4}+\frac{1-0.0411}{785})\approx 0.590\\ & b=(23.4/785{)}^{0.1}\approx 0.704\\ & C_0\approx 0.590\times [1+(1/0.590-1{)}^{0.704}]\approx 1.047\end{array}$$

$$\begin{array}{rl}& \beta \approx \frac{0.0153}{23.4}/(\frac{0.0153}{23.4}+\frac{1-0.0153}{785})\approx 0.342\\ & b=(23.4/785{)}^{0.1}\approx 0.704\\ & C_0\approx 0.342\times [1+(1/0.342-1{)}^{0.704}]\approx 0.884\end{array}$$

10. Calculate the void fraction at $Z=2\mathrm{m},\alpha (Z=2\mathrm{m})$. The void fraction is calculated by

$$⟨\alpha ⟩=\frac{⟨j_g⟩}{C_0⟨j⟩+⟨⟨v_{gj}⟩⟩}$$

where

Wrong answer

$$\begin{array}{rl}& j_g=\frac{Gx}{{\rho }_g}\approx \frac{1177.5\times 0.0411}{23.4}\mathrm{m}/\mathrm{s}\approx 2.068\mathrm{m}/\mathrm{s}\\ & j_f=\frac{G(1-x)}{{\rho }_f}\approx \frac{1177.5\times (1-0.0411)}{785}\mathrm{m}/\mathrm{s}\approx 1.438\mathrm{m}/\mathrm{s}\\ & j=j_g+j_f\approx (2.068+1.438)\mathrm{m}/\mathrm{s}\approx 3.507\mathrm{m}/\mathrm{s}.\end{array}$$

$$\begin{array}{rl}& j_g=\frac{Gx}{{\rho }_g}\approx \frac{1177.5\times 0.153}{23.4}\mathrm{m}/\mathrm{s}\approx 0.769\mathrm{m}/\mathrm{s}\\ & j_f=\frac{G(1-x)}{{\rho }_f}\approx \frac{1177.5\times (1-0.153)}{785}\mathrm{m}/\mathrm{s}\approx 1.477\mathrm{m}/\mathrm{s}\\ & j=j_g+j_f\approx (0.769+1.477)\mathrm{m}/\mathrm{s}\approx 2.246\mathrm{m}/\mathrm{s}\\ & ⟨⟨v_{gj}⟩⟩=2.9{\left(\frac{\mathrm{\Delta }\rho g\sigma }{{\rho }_f^2}\right)}^{0.25}=2.9\times {\left[\frac{(785-23.4)\times 9.8\times 0.0329}{{785}^2}\right]}^{0.25}\mathrm{m}/\mathrm{s}\approx 0.410\mathrm{m}/\mathrm{s}.\end{array}$$

Thus

Wrong answer

$$⟨\alpha ⟩\approx \frac{0.769}{0.884\times 2.246+0.410}\approx 0.507.$$

$$⟨\alpha ⟩\approx \frac{2.068}{1.047\times 3.507+0.410}\approx 0.321.$$