4 Determinants

The determinant is a scalar-valued function defined on the set of square matrices. Although the determinant is not a linear transformation on ${\mathsf{M}}_{n\times n}(F)$ for $n>1$, it does possess a kind of linearity (called $n$-linearity) as well as other properties that are examined in this chapter.

It represents the scaling factor of volume (or area in 2D) under the associated linear transformation.

4.1 Determinants of Order 2

Definition: determinant of $2\times 2$ matrices

If

$$A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right),$$

then the determinant of $A$ is

$$det(A)=ad-bc.$$

Example 4.1.1

For matrices

$$A=\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right),B=\left(\begin{array}{cc}3& 2\\ 6& 4\end{array}\right)\in {\mathsf{M}}_{2\times 2}(\mathbb{R}),$$

we have

$$det(A)=1\cdot 4-2\cdot 3=-2,$$$$det(B)=3\cdot 4-2\cdot 6=0.$$

The function $det:{\mathsf{M}}_{2\times 2}(\mathbb{R})\to \mathbb{R}$ is not linear as

$$det(A+B)\ne det(A)+det(B).$$

Nevertheless, the determinant does possess an important linearity property.

Meaning of determinant of order 2

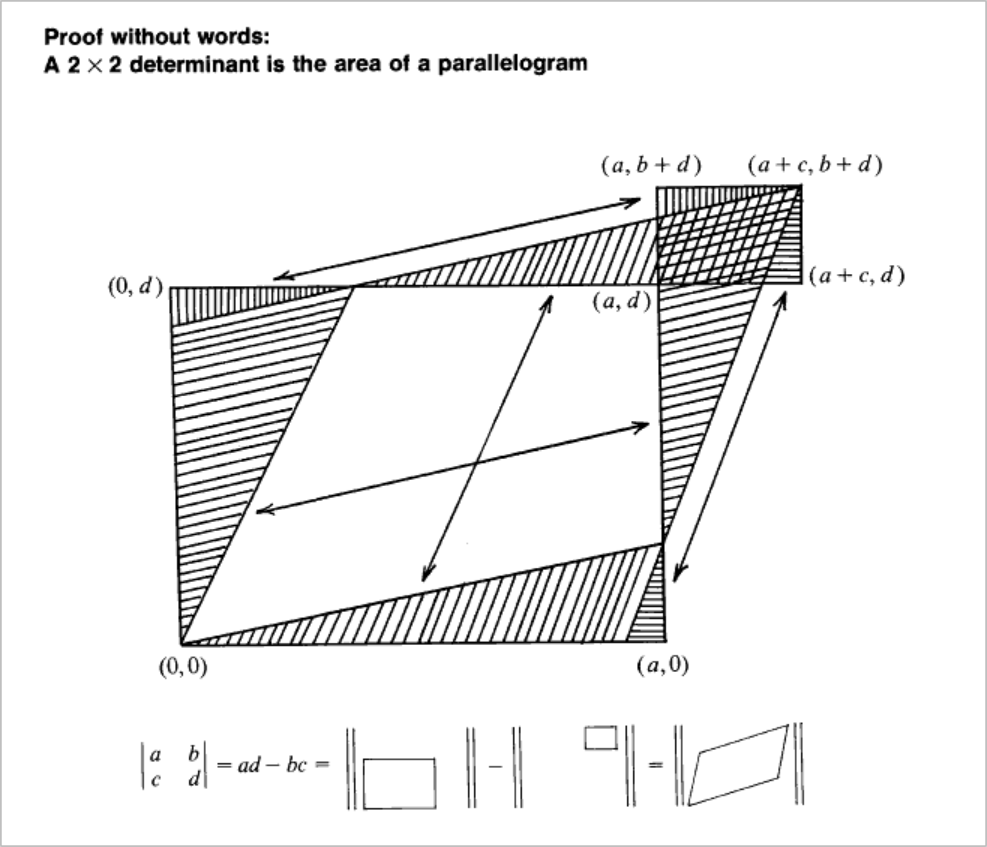
The vectors represented by a 2-by-2 matrix correspond to the sides of a unit square transformed into a parallelogram. The matrix $A$ is said to represent the linear map $f$, and $A$ is called the transformation matrix of $f$.

A determinant of $0$ would mean that all of space is squished onto something with $0$ volume, meaning (dimension is $3$)either a flat plane, a line, or, in the most extreme case, onto a single point.

Theorem 4.1

The function $det:{\mathsf{M}}_{2\times 2}(F)\to F$ is linear in each row when the other row is fixed. That is, for vectors $u,v,w\in {\mathsf{F}}^2$ and scalar $k$,

$$det(u+kv,w)=det(u,w)+kdet(v,w),$$

and similarly for the second row:

$$det(w,u+kv)=det(w,u)+kdet(w,v),$$

Theorem 4.2

For $A\in {\mathsf{M}}_{2\times 2}(F)$, $det(A)$ is nonzero if and only if $A$ is invertible. Furthermore,

$$A^{-1}=\frac{1}{det(A)}\left(\begin{array}{cc}{A}_{22}& -A_{12}\\ -A_{21}& A_{11}\end{array}\right).$$

4.2 Determinants of order $n$

Definition

Let $A\in {\mathrm{M}}_{n\times n}(F)$. If $n=1$, so that $A=\left(A_{11}\right)$, we define $\det (A)=A_{11}$. For $n\ge 2$, we define $\det (A)$ recursively as

$$\det (A)=\sum _{j=1}^n(-1{)}^{1+j}{A}_{1j}\cdot \det \left({\tilde{A}}_{1j}\right)$$

The scalar $\det (A)$ is called the determinant of $A$ and is also denoted by $|A|$. The scalar

$$(-1{)}^{i+j}\det \left({\tilde{A}}_{ij}\right)$$

is called the cofactor of the entry of $A$ in row $i$, column $j$. Letting

$$c_{ij}=(-1{)}^{i+j}\det \left({\tilde{A}}_{ij}\right)$$

denote the cofactor of the row $i$, column $j$ entry of $A$, we can express the formula for the determinant of $A$ as

$$\det (A)=A_{11}{c}_{11}+A_{12}{c}_{12}+\cdots +A_{1n}{c}_{1n}$$

Thus the determinant of $A$ equals the sum of the products of each entry in row 1 of $A$ multiplied by its cofactor. This formula is called cofactor expansion along the first row of $A$. Note that, for $2\times 2$ matrices, this definition of the determinant of $A$ agrees with the one given in Section 4.1 because

$$\begin{array}{rl}\det (A)& =A_{11}(-1{)}^{1+1}\det \left({\tilde{A}}_{11}\right)+A_{12}(-1{)}^{1+2}\det \left({\tilde{A}}_{12}\right)\\ & =A_{11}{A}_{22}-A_{12}{A}_{21}\end{array}$$

Example 4.2.1 (3x3 Matrix determinant)

For

$$A=\left(\begin{array}{ccc}1& 3& -3\\ -3& -5& 2\\ 4& -6& -4\end{array}\right),$$

Using cofactor expansion along the first row of $A$, we obtain,

$$\begin{array}{rl}\det (A)=& (-1{)}^{1+1}{A}_{11}\cdot det({\tilde{A}}_{11})+(-1{)}^{1+2}{A}_{12}\cdot det({\tilde{A}}_{12})\\ & +(-1{)}^{1+3}{A}_{13}\cdot det({\tilde{A}}_{13})\\ =& (-1{)}^2(1)\cdot det\left(\begin{array}{cc}-5& 2\\ 4& -6\end{array}\right)+(-1{)}^3(3)\cdot \left(\begin{array}{cc}-3& 2\\ -4& -6\end{array}\right)\\ & +(-1{)}^4(-3)\cdot det\left(\begin{array}{cc}-3& -5\\ -4& 4\end{array}\right)\\ =& 1[-5(-6)-2(4)]-3[-3(-6)-2(-4)]\\ & -3[-3(4)-(-5)(-4)]\\ =& 1(22)-3(26)-3(-32)\\ =& 40.\end{array}$$

Example 4.2.2

Calculate determinant of

$$B=\left(\begin{array}{ccc}0& 1& 3\\ -2& -3& -5\\ 4& -4& 4\end{array}\right),$$

Using cofactor expansion along the first row of $B$, we obtain,

$$\begin{array}{rl}\det (B)=& (-1{)}^{1+1}{B}_{11}\cdot det({\tilde{B}}_{11})+(-1{)}^{1+2}{B}_{12}\cdot det({\tilde{B}}_{12})\\ & +(-1{)}^{1+3}{B}_{13}\cdot det({\tilde{B}}_{13})\\ =& (-1{)}^2(0)\cdot det\left(\begin{array}{cc}-3& -5\\ -4& 4\end{array}\right)+(-1{)}^3(1)\cdot det\left(\begin{array}{cc}-2& -5\\ 4& 4\end{array}\right)\\ & +(-1{)}^4(3)\cdot det\left(\begin{array}{cc}-2& -3\\ 4& -4\end{array}\right)\\ =& 0-1[-2(4)-(-5)(4)]+3[-2(-4)-(-3)(4)]\\ =& 0-1(12)+3(20)\\ =& 48.\end{array}$$

Example 4.2.3

For

$$C=\left(\begin{array}{cccc}2& 0& 0& 0\\ 0& 1& 3& -3\\ 2& -3& -5& 2\\ 1& 4& -4& -6\end{array}\right),$$

Using cofactor expansion along the first row of $C$ and the results of Examples 4.2.1 and 4.2.2, we obtain,

$$\begin{array}{rl}\det (C)=& (-1{)}^2(2)\cdot det({\tilde{C}}_{11})+(-1{)}^3(0)\cdot det({\tilde{C}}_{12})\\ & +(-1{)}^4(0)\cdot \det ({\tilde{C}}_{13})+(-1{)}^5(1)\cdot \det ({\tilde{C}}_{14})\\ =& (-1{)}^2(2)\cdot det\left(\begin{array}{ccc}1& 3& -3\\ -3& -5& 2\\ -4& 4& -6\end{array}\right)+0+0\\ & +(-1{)}^5(1)\cdot det\left(\begin{array}{ccc}0& 1& 3\\ -2& -3& -5\\ 4& -4& 4\end{array}\right)\\ =& 2(40)+0+0-1(48)\\ =& 32.\bullet \end{array}$$

Example 4.2.4

The determinant of the $n\times n$ identity matrix is 1 . We prove this assertion by mathematical induction on $n$. The result is clearly true for the $1\times 1$ identity matrix. Assume that the determinant of the $(n-1)\times (n-1)$ identity matrix is 1 for some $n\ge 2$, and let $I$ denote the $n\times n$ identity matrix. Using cofactor expansion along the first row of $I$, we obtain

$$\begin{array}{rl}\det (I)=& (-1{)}^2(1)\cdot \det \left({\tilde{I}}_{11}\right)+(-1{)}^3(0)\cdot \det \left({\tilde{I}}_{12}\right)+\cdots \\ & +(-1{)}^{1+n}(0)\cdot \det \left({\tilde{I}}_{1n}\right)\\ =& 1(1)+0+\cdots +0\\ =& 1\end{array}$$

because ${\tilde{I}}_{11}$ is the $(n-1)\times (n-1)$ identity matrix. This shows that the determinant of the $n\times n$ identity matrix is 1 , and so the determinant of any identity matrix is 1 by the principle of mathematical induction.

Theorem

Theorem 4.3

The determinant of an $n\times n$ matrix is a linear function of each row when other rows are fixed. That is, for $1\le r\le n$, we have

$$det\left(\begin{array}{c}{a}_1\\ ⋮\\ a_{r-1}\\ u+kv\\ a_{r+1}\\ ⋮\\ a_n\end{array}\right)=det\left(\begin{array}{c}{a}_1\\ ⋮\\ a_{r-1}\\ u\\ a_{r+1}\\ ⋮\\ a_n\end{array}\right)+kdet\left(\begin{array}{c}{a}_1\\ ⋮\\ a_{r-1}\\ v\\ a_{r+1}\\ ⋮\\ a_n\end{array}\right)$$

whenever $k$ is a scalar and $u,v$ and each $a_i$ are row vectors in ${\mathsf{F}}^n$.

Corollary

If an $n\times n$ matrix has a row consisting entirely of zeros, then its determinant is zero.

Theorem 4.4

The determinant can be computed by cofactor expansion along any row $i$:

$$det(A)=\sum _{j=1}^n(-1{)}^{i+j}{A}_{ij}det({\tilde{A}}_{ij}).$$

Corollary

If a matrix has two identical rows, then its determinant is zero.

Theorem 4.5

If $B$ is obtained from $A$ by interchanging two rows, then

$$det(B)=-det(A).$$

We now complete our investigation of how an elementary row operation affects the determinant of a matrix by showing that elementary row operations of type 3 do not change the determinant of a matrix.

Theorem 4.6

If $B$ is obtained from $A$ by adding a multiple of one row to another, then

$$det(B)=det(A).$$

Corollary

If $A$ has rank less than $n$, then $det(A)=0$.

Rules for Elementary Row Operations on Determinants:

• Interchange two rows: determinant changes sign.
• Multiply a row by scalar $k$: determinant multiplied by $k$.
• Add a multiple of one row to another: determinant unchanged.

Exammple 4.2.5

To evaluate the determinant of the matrix

$$B=\left(\begin{array}{rrr}0& 1& 3\\ -2& -3& -5\\ 4& -4& 4\end{array}\right)$$

in Example 2, we must begin with a row interchange. Interchanging rows 1 and 2 of $B$ produces

$$C=\left(\begin{array}{rrr}-2& -3& -5\\ 0& 1& 3\\ 4& -4& 4\end{array}\right)$$

By means of a sequence of elementary row operations of type 3, we can transform $C$ into an upper triangular matrix:

$$\begin{array}{rl}& \left(\begin{array}{rrr}-2& -3& -5\\ 0& 1& 3\\ 4& -4& 4\end{array}\right)⟶\left(\begin{array}{rrr}-2& -3& -5\\ 0& 1& 3\\ 0& -10& -6\end{array}\right)\\ ⟶& \left(\begin{array}{rrr}-2& -3& -5\\ 0& 1& 3\\ 0& 0& 24\end{array}\right).\end{array}$$

Thus $\det (C)=-2\cdot 1\cdot 24=-48$. Since $C$ was obtained from $B$ by an interchange of rows, it follows that

$$\det (B)=-\det (C)=48.$$

Example 4.2.6

The technique in Example 4.2.5 can be used to evaluate the determinant of the matrix

$$C=\left(\begin{array}{rrrr}2& 0& 0& 1\\ 0& 1& 3& -3\\ -2& -3& -5& 2\\ 4& -4& 4& -6\end{array}\right)$$

in Example 4.2.3, This matrix can be transformed into an upper triangular matrix by means of the following sequence of elementary row operations of type 3:

$$\begin{array}{rl}& \left(\begin{array}{rrrr}2& 0& 0& 1\\ 0& 1& 3& -3\\ -2& -3& -5& 2\\ 4& -4& 4& -6\end{array}\right)⟶\left(\begin{array}{rrrr}2& 0& 0& 1\\ 0& 1& 3& -3\\ 0& -3& -5& 3\\ 0& -4& 4& -8\end{array}\right)\\ ⟶& \left(\begin{array}{rrrr}2& 0& 0& 1\\ 0& 1& 3& -3\\ 0& 0& 4& -6\\ 0& 0& 16& -20\end{array}\right)⟶\left(\begin{array}{rrrr}2& 0& 0& 1\\ 0& 1& 3& -3\\ 0& 0& 4& -6\\ 0& 0& 0& 4\end{array}\right).\end{array}$$

Thus $\det (C)=2\cdot 1\cdot 4\cdot 4=32$ .

4.3 Properties of Determinants

The determinant of elementary matrices:

(a) Type 1 (row interchange): determinant = $-1$.

(b) Type 2 (row scaling): determinant = scalar $k$.

(c) Type 3 (row addition): determinant = $1$.

Theorem 4.7 [core]

For any $A,B\in {\mathsf{M}}_{n\times n}(F)$,

$$det(AB)=det(A)\cdot det(B).$$

Corollary

Matrix $A$ is invertible if and only if

$$det(A)\ne 0,$$

and if invertible,

$$det(A^{-1})=\frac{1}{det(A)}.$$

Theorem 4.8

For any $A\in {\mathsf{M}}_{n\times n}(F)$,

$$det(A^{\mathrm{\top }})=det(A).$$

Cramer's Rule [core]

Theorem 4.9 Cramer's Rule

Let $Ax=b$ be a system of $n$ linear equations in $n$ unknowns. If $det(A)\ne 0$, then the system has a unique solution, and for each $k$ ($1\le k\le n$),

$$x_k=\frac{det(M_k)}{det(A)},$$

where $M_k$ is the matrix obtained from $A$ by replacing column $k$ by $b$.

Example 4.3.1 (Applying Cramer's Rule):

Solve the system

$$\{\begin{array}{l}{x}_1+2x_2+3x_3=2\\ x_1+x_3=3\\ x_2+2x_3=1\end{array}$$

Matrix form: $Ax=b$, where

$$A=\left(\begin{array}{ccc}1& 2& 3\\ 1& 0& 1\\ 0& 1& 2\end{array}\right),b=\left(\begin{array}{c}2\\ 3\\ 1\end{array}\right)$$

Since $det(A)=6\ne 0$, the system has a unique solution:

$$\begin{array}{rl}& x_1=\frac{\det (M_1)}{\det (A)}=\frac{det\left(\begin{array}{ccc}2& 2& 3\\ 3& 0& 1\\ 1& 1& -1\end{array}\right)}{det(A)}=\frac{15}{6}=\frac{5}{2},\\ & x_2=\frac{det(M_2)}{det(A)}=\frac{det\left(\begin{array}{ccc}1& 2& 3\\ 1& 3& 1\\ 1& 1& -1\end{array}\right)}{det(A)}=\frac{-6}{6}=-1,\\ & x_3=\frac{\det (M_3)}{\det (A)}=\frac{\det \left(\begin{array}{ccccc}1& & 2& & 2\\ 1& & 0& & 3\\ 1& & 1& & 1\end{array}\right)}{\det (A)}=\frac{3}{6}=\frac{1}{2}.\end{array}$$

Thus the unique solution to the given system of the linear equation is

$$(x_1,x_2,x_3)=(\frac{5}{2},-1,\frac{1}{2}).$$

Geometric Interpretations of Determinants

• $det(A)\ne 0$: The matrix $A$ corresponds with some linear transformation, so solving $Ax=v$ means we‘re looking for a vector $x$, which, after applying the transformation, lands on $v$.

• $det(A)=0$: When it squishes 3D space onto the plane, or even if it squishes it onto a line or a point. Those all correspond to a determinant of zero, since any region is squished into something with zero volume. It's still possible that a solution exists even when there is no inverse.

• The absolute value of $det(A)$ equals the $n$-dimensional volume of the parallelepiped formed by the rows (or columns) of $A$.

• $det(A)=0$ means the volume collapses to zero, i.e., the vectors are linearly dependent.

• Changing basis orientation changes the sign of $det(A)$.

it is possible to interpret the determinant of a matrix $A\in {\mathsf{M}}_{n\times n}(\mathbb{R})$ geometrically. If the rows of $A$ are $a_1,a_2,\dots ,a_n$, respectively, then $|\det (A)|$ is the $n$-dimensional volume (the generalization of area in ${\mathbb{R}}^2$ and volume in ${\mathbb{R}}^3$ ) of the parallelepiped having the vectors $a_1,a_2,\dots ,a_n$ as adjacent sides.

Example 4.3.2

The volume of the parallelepiped having the vectors $a_1=(1,-2,1),a_2=(1,0,-1)$, and $a_3=(1,1,1)$ as adjacent sides is

$$\left|\det \left(\begin{array}{rrr}1& -2& 1\\ 1& 0& -1\\ 1& 1& 1\end{array}\right)\right|=6$$

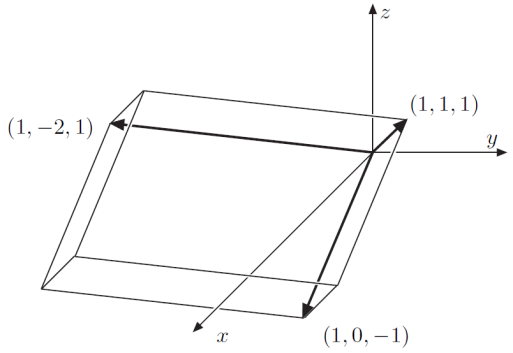
Note that the object in question is a rectangular parallelepiped (see Figure 4.6 ) with sides of lengths $\sqrt{6},\sqrt{2}$, and $\sqrt{3}$. Hence by the familiar formula for volume, its volume should be $\sqrt{6}\cdot \sqrt{2}\cdot \sqrt{3}=6$, as the determinant calculation shows.

row reducing and relationship

$$\begin{array}{rl}& \{\begin{array}{c}ax+by+cz=u\\ dx+ey+fz=v\\ gx+hy+iz=w\end{array}\\ & \left[\begin{array}{lll}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]\stackrel{\frac{1}{a}{R}_1\to R_1}{\to }\left[\begin{array}{lll}1& \frac{b}{a}& \frac{c}{a}\\ d& e& f\\ g& h& i\end{array}\right]\\ \stackrel{\begin{array}{c}-d{R}_1+R_2\to R_2\\ -g{R}_1+R_3\to R_3\end{array}}{\to }& \left[\begin{array}{ccc}1& \frac{b}{a}& \frac{c}{a}\\ 0& \frac{ae-bd}{a}& \frac{af-cd}{a}\\ 0& \frac{ah-bg}{a}& \frac{ai-cg}{a}\end{array}\right]\end{array}$$

Continuing,

$$\left[\begin{array}{ccc}1& \frac{b}{a}& \frac{c}{a}\\ 0& \frac{ac-bd}{a}& \frac{af-cd}{a}\\ 0& \frac{ah-bq}{a}& \frac{ai-cq}{a}\end{array}\right]\stackrel{\begin{array}{l}\frac{a}{ac-bd}{R}_2\to R_2\\ \frac{a}{ah-bg}{R}_3\to R_3\end{array}}{\to }\left[\begin{array}{ccc}1& \frac{b}{a}& \frac{c}{a}\\ 0& 1& \frac{af-cd}{ac-bd}\\ 0& 1& \frac{ai-cg}{ah-bg}\end{array}\right]$$

And,

$$\left[\begin{array}{ccc}1& \frac{b}{a}& \frac{c}{a}\\ 0& 1& \frac{af-cd}{ac-bd}\\ 0& 1& \frac{ai-cg}{ah-bg}\end{array}\right]\stackrel{-R_2+R_3\to R_3}{\to }\left[\begin{array}{ccc}1& \frac{b}{a}& \frac{c}{a}\\ 0& 1& \frac{af-cd}{ac-bd}\\ 0& 0& \frac{(ai-cg)(ae-bd)-(af-cd)(ah-bg)}{(ah-bg)(ae-bd)}\end{array}\right]$$

Relationship to the Determinant

Note that we are also assuming that $ah-bg\ne 0$ and $ae-bd\ne 0$ in the preceding computations.

Now the question is this. Under what condition on the quantity in the lower right corner of this last matrix will the original system be guaranteed to not have a unique solution? This would mean it would have no solutions or infinitely many.

Remember that the quantity in the lower right corner of the last matrix above is the coefficient of $z$ in the row equivalent system that corresponds to the REF form. This new system is guaranteed to not have a unique solution if that coefficient is zero. Make sure you think about why this makes sense!

Therefore, the condition for lack of a unique solution is $(ai-cg)(ae-bd)-(af-cd)(ah-bg)=0$. By expansion, this is equivalent to the equation

$$a^{2}ei-abdi-aceg+bcdg-(a^{2}fh-abfg-acdh+bcdg)=0$$

But this simplifies to $a(aei-bdi-ceg-afh+bfg+cdh)=0$. Since we are assuming that $a\ne 0$, this is equivalent to

$$aei-afh-bdi+bfg+cdh-ceg=a(ei-fh)-b(di-fg)+c(dh-eg)=0.$$

But the expression $a(ei-fh)-b(di-fg)+c(dh-eg)$ is the determinant of the $3\times 3$ coefficient matrix of the system!

Ultimately, we can say that the original linear system of three equations and three unknowns has a unique solution if and only if the determinant of its $3\times 3$ coefficient matrix is nonzero.