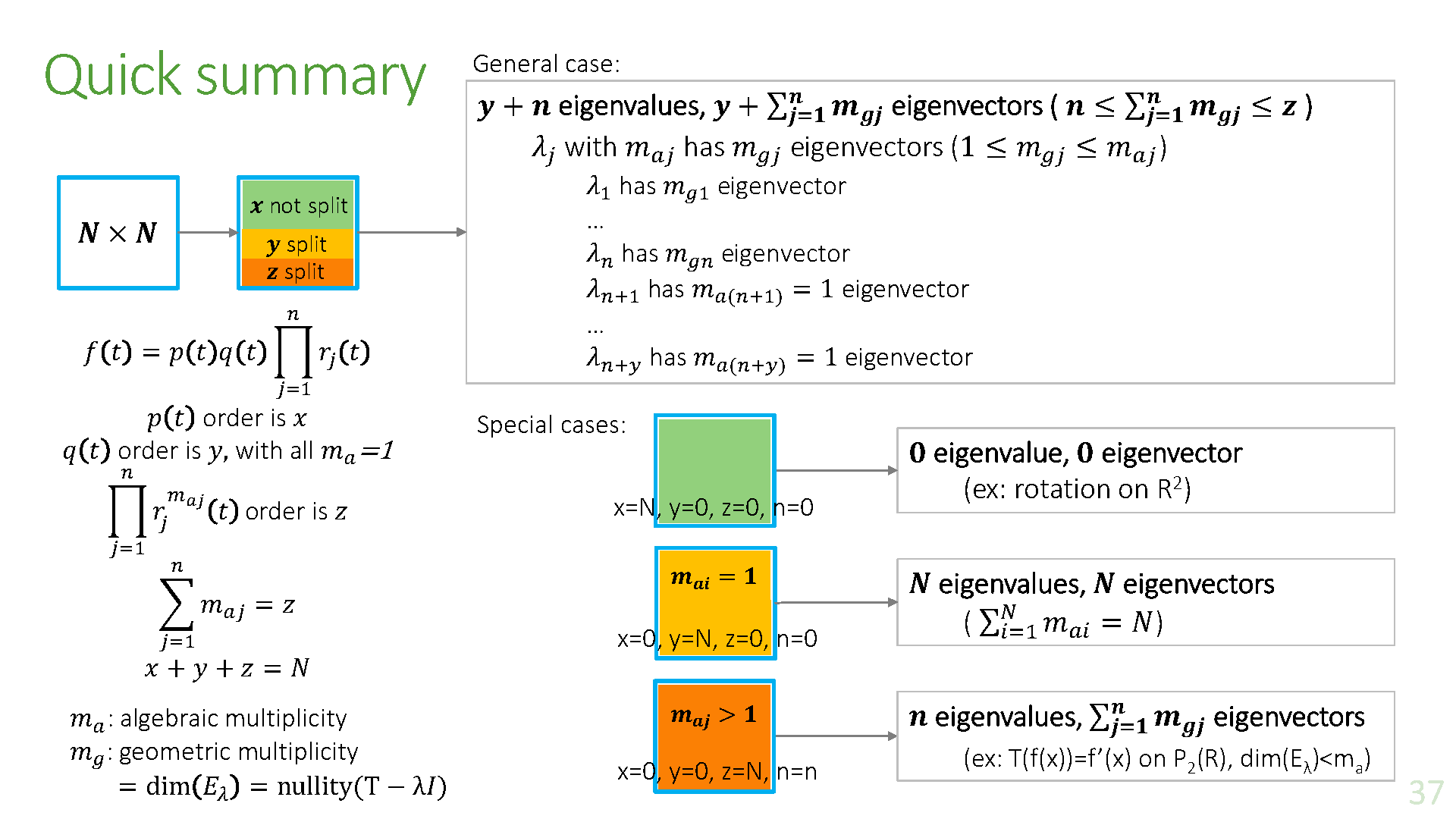
5 Eigenvalues and Eigenvectors

5.1 Eigenvalues and Eigenvectors

Definition and Theorem

This chapter is concerned with the so-called diagonalization problem. For a given linear operator $\mathsf{T}$ on a finite-dimensional vector space $\mathsf{V}$, we seek answers to the following questions.

1. Does there exist an ordered basis $\beta$ for $\mathsf{V}$ such that $[T{]}_{\beta }$ is a diagonal matrix?
2. If such a basis exists, how can it be found?

Definitions: diagonalizable

A linear operator $\mathsf{T}$ on a finite-dimensional vector space $\mathsf{V}$ is called diagonalizable if there is an ordered basis $\beta$ for $\mathsf{V}$ such that $[\mathsf{T}{]}_{\beta }$ is a diagonal matrix. A square matrix $A$ is called diagonalizable if ${\mathsf{L}}_A$ is diagonalizable.

Definitions: eigenvalue & eigenvector

Let $\mathsf{T}$ be a linear operator on a vector space $\mathsf{V}$. A nonzero vector $v\in \mathsf{V}$ is called an eigenvector of $\mathsf{T}$ if there exists a scalar $\lambda$ such that $\mathsf{T}(v)=\lambda v$. The scalar $\lambda$ is called the eigenvalue corresponding to the eigenvector $\mathsf{V}$.

Let $A$ be in ${\mathsf{M}}_{n\times n}(F)$. A nonzero vector $v\in {\mathsf{F}}^n$ is called an eigenvector of $A$ if $v$ is an eigenvector of ${\mathsf{L}}_A$; that is, if $Av=\lambda v$ for some scalar $\lambda$. The scalar $\lambda$ is called the eigenvalue of $A$ corresponding to the eigenvector $\mathsf{V}$.

Theorem 5.1

A linear operator $\mathsf{T}$ on a finite-dimensional vector space $\mathsf{V}$ is diagonalizable if and only if there exists an ordered basis $\beta$ for $\mathsf{V}$ consisting of eigenvectors of $\mathsf{T}$.

Furthermore, if $\mathsf{T}$ is diagonalizable, $\beta =\{v_1,v_2,...,v_n\}$ is an ordered basis of eigenvectors of $\mathsf{T}$, and $D=[T{]}_{\beta }$, then $D$ is a diagonal matrix and $D_{jj}$ is the eigenvalue corresponding to $v_j$ for $1\le j\le n$.

Corollary

A matrix $A\in {\mathsf{M}}_{n\times n}(F)$ is diagonalizable if and only if there exists an ordered basis for $F^n$ consisting of eigenvectors of $A$. Furthermore, if $\{v_1,v_2,...,v_n\}$ is an ordered basis for ${\mathsf{F}}^n$ consisting of eigenvectors of $A$ and $Q$ is the $n\times n$ matrix whose $j$th column is $v_j$ for $j=1,2,...,n$, then $D=Q^{-1}AQ$ is a diagonal matrix such that $D_{jj}$ is the eigenvalue of $A$ corresponding to $v_j$. Hence $A$ is diagonalizable if and only if it is similar to a diagonal matrix.

$$[\mathsf{T}{]}_{\beta }=\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_n\end{array}\right]$$

Example 5.1.1

Let

$$A=\left[\begin{array}{cc}1& 3\\ 4& 2\end{array}\right],{\mathit{v}}_1=\left[\begin{array}{c}1\\ -1\end{array}\right],{\mathit{v}}_2=\left[\begin{array}{c}3\\ 4\end{array}\right].$$

Since

$${\mathsf{L}}_A({\mathit{v}}_1)=A{\mathit{v}}_1=\left[\begin{array}{cc}1& 3\\ 4& 2\end{array}\right]\left[\begin{array}{c}1\\ -1\end{array}\right]=\left[\begin{array}{c}-2\\ 2\end{array}\right]=-2\left[\begin{array}{c}1\\ -1\end{array}\right]=-2{\mathit{v}}_1$$

${\mathit{v}}_1$ is an eigenvector of ${\mathsf{L}}_A$, and hence of $A$. Here ${\lambda }_1=-2$ is the eigenvalue corresponding to ${\mathit{v}}_1$. Furthermore,

$${\mathsf{L}}_A({\mathit{v}}_2)=A{\mathit{v}}_2=\left[\begin{array}{cc}1& 3\\ 4& 2\end{array}\right]\left[\begin{array}{c}3\\ 4\end{array}\right]=\left[\begin{array}{c}15\\ 20\end{array}\right]=5\left[\begin{array}{c}3\\ 4\end{array}\right]=5{\mathit{v}}_2,$$

and so ${\mathit{v}}_2$ is an eigenvector of ${\mathsf{L}}_A$, and hence of $A$, with the corresponding eigenvalue ${\lambda }_2=5$. Note that $\beta =\{{\mathit{v}}_1,{\mathit{v}}_2\}$ is an ordered basis for ${\mathbb{R}}^2$ consisting of eigenvectors of both $A$ and ${\mathsf{L}}_A$, and therefore $A$ and ${\mathsf{L}}_A$ are diagonalizable. Moreover, by Theorem 5.1 and its corollary, if

$$Q=\left[\begin{array}{cc}2& 3\\ -1& 4\end{array}\right]$$

then

$$Q^{-1}AQ=[{\mathsf{L}}_A{]}_{\beta }=\left[\begin{array}{cc}-2& 0\\ 0& 5\end{array}\right]$$

Example 5.1.2

Let $\mathsf{T}$ be the linear operator on ${\mathbb{R}}^2$ that rotates each vector in the plane through an angle of $\pi /2$.

It is clear geometrically that for any nonzero vector $v$, the vector $\mathsf{T}(v)$ does not lie on the line through 0 determined by $v$ (geometrical meaning of eigenvector, but for this $\mathsf{T}$); hence $\mathsf{T}(v)$ is not a multiple of $v$. Therefore $\mathsf{T}$ has no eigenvectors and, consequently, no eigenvalues. Thus there exist operators (and matrices) with no eigenvalues or eigenvectors. Of course, such operators and matrices are not diagonalizable.

While in the field of complex number ${\mathbb{C}}^2$, it exists:

$$A=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$$$p_A(t)=det(A-tI)=t^2-2(\cos \theta )t+1$$$$e^{\pm i\theta }=\cos \theta \pm i\sin \theta ,{\lambda }_1=e^{i\theta },{\lambda }_2=e^{-i\theta }$$

For basis $\beta =\{x_1,x_2\}$,

$$[A{]}_{\beta }=\left[\begin{array}{cc}{e}^{i\theta }& 0\\ 0& e^{-i\theta }\end{array}\right]$$

Let

$$\mathit{x}=c_1{\mathit{x}}_1+c_2{\mathit{x}}_2,[\mathit{x}{]}_{\beta }=(c_1,c_2{)}^{\mathrm{\top }}$$

Then

$$[A\mathit{x}{]}_{\beta }=[A{]}_{\beta }[\mathit{x}{]}_{\beta }=[c_1{e}^{i\theta },c_2{e}^{-i\theta }{]}^{\mathrm{\top }}.$$

Example 5.1.3

Let $C^{\mathrm{\infty }}(\mathbb{R})$ denote the set of all functions $f:\mathbb{R}\to \mathbb{R}$ having derivatives of all orders(including the polynominl functions, the sine an cosine functions, the exponential functions, etc.). Clearly, $C^{\mathrm{\infty }}(\mathbb{R})$ is a subspace of the vector space $\mathcal{F}(\mathbb{R},\mathbb{R})$ of all functions from $\mathbb{R}$ to $\mathbb{R}$ as defined in Section 1.2.

Let $\mathsf{T}:C^{\mathrm{\infty }}(\mathbb{R})\to C^{\mathrm{\infty }}(\mathbb{R})$ be the function defined by $\mathsf{T}(f)=f^{\prime }$, the derivative of $f$. It's easily verified that $\mathsf{T}$ is a linear operator on $C^{\mathrm{\infty }}(\mathbb{R})$. We determine the eigenvalues and eigenvectors of $\mathsf{T}$.

Suppose $f$ is an eigenvector of $\mathsf{T}$ with eigenvalue $\lambda$. Then $f^{\prime }=\lambda f$. This's a 1st-order differential equation whose solutions are of the form $f(t)=c{e}^{\lambda t}$ for some constant $c$. Consequently, every real number $\lambda$ is an eigenvalue of $\mathsf{T}$, and corresponds to eigenvectors of the form $c{e}^{\lambda t}$ for $c\ne 0$. Note that for $\lambda =0$, the eigevectors are the nonzero constant functions, i.e. $c$.

(Here, the function $f$ is the eigenvector $v$ in $Av=\lambda v$)

Theorem 5.2

Let $A\in M_{n\times n}(F)$. A scalar $\lambda$ is an eigenvalue of $A$ if and only if

$$det(A-\lambda I_n)=0$$

Definition: characteristic polynomial (For matrix)

The polynomial $f(t)=det(A-t{I}_n)$ is called the characteristic polynomial of $A$.

Definition: characteristic polynomial (For linear transformation)

Let $\mathsf{T}$ be a linear operator on an $n$-dimensional vector space $\mathsf{V}$ with ordered basis $\beta$. We define the characteristic polynomial $f(t)$ of $\mathsf{T}$ to be the characteristic polynomial of $A=[\mathsf{T}{]}_{\beta }$. That is,

$$f(t)=det(A-t{I}_n)$$

Example 5.1.4

To find the eigenvalues of

$$A=\left[\begin{array}{cc}1& 1\\ 4& 1\end{array}\right]\in {\mathsf{M}}_{2\times 2}(\mathbb{R}),$$

we compute its characteristic polynomial:

$$\begin{array}{rl}& det(A-t{I}_2)=det\left[\begin{array}{cc}1-t& 1\\ 4& 1-t\end{array}\right]\\ =& (1-t{)}^2-4=t^2-2t-3=(t-3)(t+1).\end{array}$$

Hence, the only eigenvalues of $A$ are 3 and -1.

Example 5.1.5

Let $\mathsf{T}$ be the linear operator on ${\mathsf{P}}_2(\mathbb{R})$ defined by

$$\mathsf{T}(f(x))=f(x)+(x+1)f^{\prime }(x),$$

let $\beta$ be the standard ordered basis for ${\mathsf{P}}_2(\mathbb{R})$, and let $A=[\mathsf{T}{]}_{\beta }$. Then

$$A=\left[\begin{array}{ccc}1& 1& 0\\ 0& 2& 2\\ 0& 0& 3\end{array}\right]$$

(Explanation:

$$\begin{array}{c}f(x)=a+bx+c{x}^2\\ f^{\prime }(x)=b+2cx\\ \begin{array}{rl}\mathsf{T}(f(x))& =(a+bx+c{x}^2)+(x+1)(b+2cx)\\ & =a+bx+c{x}^2+bx+b+2c{x}^2+2cx\\ & =(a+b)+(2b+2c)x+3c{x}^2\end{array}\end{array}$$

)

The characteristic polynomial of $\mathsf{T}$ is

$$\begin{array}{rl}det(A-t{I}_3)& =\left|\begin{array}{ccc}1-t& 1& 0\\ 0& 2-t& 2\\ 0& 0& 3-t\end{array}\right|\\ & =(1-t)(2-t)(3-t)=-(t-1)(t-2)(t-3).\end{array}$$

Hence $\lambda$ is an eigenvalue of $\mathsf{T}$ if and only if $\lambda =1,2,\text{ or }3$.

Theorem 5.3

Let $A\in {\mathsf{M}}_{n\times n}(F)$.

• The characteristic polynomial of $A$ is a polynomial of degree $n$ with leading coefficient $(-1{)}^n$.
• $A$ has at most $n$ distinct eigenvalues.

Theorem 5.4

Let $\mathsf{T}$ be a linear operator on a vector space $\mathsf{V}$, and let $\lambda$ be an eigenvalue of $\mathsf{T}$. A vector $v\in \mathsf{V}$ is an eigenvector of $\mathsf{T}$ corresponding to $\lambda$ if and only if $v\ne 0$ and $v\in \mathsf{N}(\mathsf{T}-\lambda I)$.

Example 5.1.6 [core]

To find all eigenvectors of the matrix

$$A=\left[\begin{array}{cc}1& 1\\ 4& 1\end{array}\right],$$

recall $A$ has two eigenvalues ${\lambda }_1=3$ and ${\lambda }_2=-1$. We begin with eigenvectors corresponding to ${\lambda }_1=3$. Let

$$B_1=A-3I=\left[\begin{array}{cc}1-3& 1\\ 4& 1-3\end{array}\right]=\left[\begin{array}{cc}2& 1\\ 4& -2\end{array}\right].$$

A vector $\mathit{x}=(x_1,x_2{)}^T\in {\mathbb{R}}^2$ is an eigenvector corresponding to ${\lambda }_1=3$ iff $\mathit{x}\ne \mathbf{0}$ and $\mathit{x}\in \mathsf{N}({\mathsf{L}}_{B_1})$, i.e.,

$$B_1\mathit{x}=\left[\begin{array}{cc}-2& 1\\ 4& -2\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{c}-2x_1+x_2\\ 4x_1-2x_2\end{array}\right]=\mathbf{0}.$$

Clearly the set of all solutions to this equation is

$$\{t\left[\begin{array}{c}1\\ 2\end{array}\right]:t\in \mathbb{R}\}.$$

Now, suppose $\mathit{x}$ is an eigenvector corresponding to ${\lambda }_2=-1$. Let

$$B_2=A-(-1)I=A+I=\left[\begin{array}{cc}1+1& 1\\ 4& 1+1\end{array}\right]=\left[\begin{array}{cc}2& 1\\ 4& 2\end{array}\right].$$

$\mathit{x}\in \mathsf{N}({\mathsf{L}}_{B_2})$ iff

$$B_2\mathit{x}=0⟹\{\begin{array}{l}2x_1+x_2=0\\ 4x_1+2x_2=0\end{array}$$

Hence

$$\mathsf{N}({\mathsf{L}}_{B_2})=\{t\left[\begin{array}{c}1\\ -2\end{array}\right]:t\in \mathbb{R}\}.$$

Thus $\mathit{x}$ is an eigenvector corresponding to ${\lambda }_2=-1$ iff

$$\mathit{x}=t(1,-2{)}^{\mathrm{\top }}\text{for some }t\ne 0.$$

Observe that

$$\{(1,2{)}^{\mathrm{\top }},(1,-2{)}^{\mathrm{\top }}\}$$

is a basis for ${\mathbb{R}}^2$ consisting of eigenvectors of $A$. Thus ${\mathsf{L}}_A$, and hence $A$, is diagonalizable.

Suppose that $\beta$ is a basis for ${\mathsf{F}}^n$ consisting of eigenvectors of $A$. The corollary to Theorem 2.23 assures that if $Q$ is the $n\times n$ matrix whose columns are the vectors in $\beta$, then $Q^{-1}AQ$ is a diagonal matrix. For example, in Example 5.1.6, if

$$Q=\left[\begin{array}{cc}1& 1\\ 2& -2\end{array}\right],D=Q^{-1}AQ=\left[\begin{array}{cc}3& 0\\ 0& -1\end{array}\right].$$

The diagonal entries of this matrix are the eigenvalues of $A$ that correspond to the respective columns of $Q$.

To find the eigenvectors of a linear operator $\mathsf{T}$ on an $n$-dimensional vector space, select an ordered basis $\beta$ for $\mathsf{V}$ and let $A=[\mathsf{T}{]}_{\beta }$. Then for $v\in \mathsf{V}$, ${\varphi }_{\beta }(v)=[v{]}_{\beta }$, the coordinate vector of $v$ relative to $\beta$. We show that $v\in \mathsf{V}$ is an eigenvector of $\mathsf{T}$ corresponding to $\lambda$ if and only if ${\varphi }_{\beta }(v)$ is an eigenvector of $A$ corresponding to $\lambda$. Suppose $v$ is an eigenvector with eigenvalue $\lambda$, then $\mathsf{T}(v)=\lambda v$. Hence

$$A{\varphi }_{\beta }(v)={\mathsf{L}}_A{\varphi }_{\beta }\mathsf{T}(v)={\varphi }_{\beta }(\mathsf{T}(v))={\varphi }_{\beta }(\lambda v)=\lambda {\varphi }_{\beta }(v),$$

Now ${\varphi }_{\beta }(v)\ne 0$, since ${\varphi }_{\beta }$ is an isomorphism; hence ${\varphi }_{\beta }(v)$ is an eigenvector of $A$. This argument is reversible, and so we can establish that if ${\varphi }_{\beta }(v)$ is an eigenvector of $A$ corresponding to $\lambda$, then $v$ is an eigenvector of T corresponding to $\lambda$.

An equivalent formulation of the result discussed in the preceding paragraph is that for an eigenvalue $\lambda$ of $A$ (and hence of $\mathsf{T}$ ), a vector $y\in {\mathsf{F}}^n$ is an eigenvector of $A$ corresponding to $\lambda$ if and only if ${\varphi }_{\beta }^{-1}(y)$ is an eigenvector of T corresponding to $\lambda$.

We can choose to solve the problem using whichever path is easier.

Example 5.1.7

Let $\mathsf{T}$ be the linear operator on ${\mathsf{P}}_2(\mathbb{R})$ defined in Example 5.1.5, i.e., $\mathsf{T}(f(x))=f(x)+(x+1)f^{\prime }(x)$, and let $\beta$ be the standard ordered basis for ${\mathsf{P}}_2(\mathbb{R})$. Recall that $\mathsf{T}$ has eigenvalues $1,2,3$ and that

$$A=[\mathsf{T}{]}_{\beta }=\left(\begin{array}{ccc}1& 1& 0\\ 0& 2& 2\\ 0& 0& 3\end{array}\right)$$

We consider each eigenvalue separately. Let ${\lambda }_1=1$, and define

$$B_1=A-{\lambda }_{1}I=\left(\begin{array}{lll}0& 1& 0\\ 0& 1& 2\\ 0& 0& 2\end{array}\right)$$

Then

$$\mathit{x}=\left(\begin{array}{l}{x}_1\\ x_2\\ x_3\end{array}\right)\in {\mathbb{R}}^3$$

is an eigenvector corresponding to ${\lambda }_1=1$ if and only if $\mathit{x}\ne \mathbf{0}$ and $\mathit{x}\in \mathsf{N}\left({\mathsf{L}}_{B_1}\right)$; that is, $\mathit{x}$ is a nonzero solution to the system

$$\begin{array}{rlrlrl}& x_2& & & & =0\\ & x_2+& & 2x_3& & =0\\ & & & 2x_3& & =0\end{array}$$

Notice that this system has three unknowns, $x_1,x_2$, and $x_3$, but one of these, $x_1$, does not actually appear in the system. Since the values of $x_1$ do not affect the system, we assign $x_1$ a parametric value, say $x_1=a$, and solve the system for $x_2$ and $x_3$. Clearly, $x_2=x_3=0$, and so the eigenvectors of $A$ corresponding to ${\lambda }_1=1$ are of the form

$$a\left(\begin{array}{l}1\\ 0\\ 0\end{array}\right)=a{e}_1$$

for $a\ne 0$. Consequently, the eigenvectors of T corresponding to ${\lambda }_1=1$ are of the form

$${\varphi }_{\beta }^{-1}\left(a{e}_1\right)=a{\varphi }_{\beta }^{-1}\left(e_1\right)=a\cdot 1=a$$

for any $a\ne 0$. Hence the nonzero constant polynomials are the eigenvectors of $\mathsf{T}$ corresponding to ${\lambda }_1=1$.

Next let ${\lambda }_2=2$, and define

$$B_2=A-{\lambda }_{2}I=\left(\begin{array}{rrr}-1& 1& 0\\ 0& 0& 2\\ 0& 0& 1\end{array}\right)$$

It is easily verified that

$$\mathsf{N}\left({\mathsf{L}}_{B_2}\right)=\{a\left(\begin{array}{l}1\\ 1\\ 0\end{array}\right):a\in R\},$$

and hence the eigenvectors of $\mathsf{T}$ corresponding to ${\lambda }_2=2$ are of the form

$${\varphi }_{\beta }^{-1}\left(a\left(\begin{array}{l}1\\ 1\\ 0\end{array}\right)\right)=a{\varphi }_{\beta }^{-1}(e_1+e_2)=a(1+x)$$

for $a\ne 0$. Finally, consider ${\lambda }_3=3$ and

$$B_3=A-{\lambda }_{3}I=\left(\begin{array}{rrr}-2& 1& 0\\ 0& -1& 2\\ 0& 0& 0\end{array}\right)$$

Since

$$\mathsf{N}\left({\mathsf{L}}_{B_3}\right)=\{a\left(\begin{array}{l}1\\ 2\\ 1\end{array}\right):a\in R\}$$

the eigenvectors of $\mathsf{T}$ corresponding to ${\lambda }_3=3$ are of the form

$${\varphi }_{\beta }^{-1}\left(a\left(\begin{array}{l}1\\ 2\\ 1\end{array}\right)\right)=a{\varphi }_{\beta }^{-1}(e_1+2e_2+e_3)=a(1+2x+x^2)$$

for $a\ne 0$.

For each eigenvalue, select the corresponding eigenvector with $a=1$ in the preceding descriptions to obtain $\gamma =\{1,1+x,1+2x+x^2\}$, which is an ordered basis for ${\mathsf{P}}_2(R)$ consisting of eigenvectors of $\mathsf{T}$ . Thus $\mathsf{T}$ is diagonalizable, and

$$[\mathsf{T}{]}_{\gamma }=\left(\begin{array}{ccc}1& 0& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right)$$

5.2 Diagonalizability

Theorem 5.5 and Corollary

What is still needed is a simple test to determine whether an operator or a matrix can be diagonalized, as well as a method for actually finding a basis of eigenvectors.

Theorem 5.5

Let $\mathsf{T}$ be a linear operator on a vector space, and let ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k$ be distinct eigenvalues of $\mathsf{T}$. For each $i=1,2,\dots ,k,$ let $S_i(i=1,2,\cdots ,k)$ be a finite set of eigenvectors of $\mathsf{T}$ corresponding to ${\lambda }_i$. If each $S_i$ is linearly independent, then $S_1\cup S_2\cup \cdots \cup S_k$ is also linearly independent.

Corollary

Let $\mathsf{T}$ be a linear operator on an $n$-dimensional vector space $\mathsf{V}$. If $\mathsf{T}$ has $n$ distinct eigenvalues, then $\mathsf{T}$ is diagonalizable.

Example 5.2.1

Let

$$A=\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]\in {\mathsf{M}}_{2\times 2}(\mathbb{R}).$$

The characteristic polynomial of $A$ ( and hence of ${\mathsf{L}}_A$) is $t(t-2)$, giving two distinct eigenvalues ${\lambda }_1=0$ and ${\lambda }_2=2$. By the corollary to Theorem 5.5, $A$ is diagonalizable for ${\mathsf{L}}_A$ is a linear operator on the 2-dimensional vector space ${\mathbb{R}}^2$.

split

Definition: split over

A polynomial $f(t)$ in $\mathsf{P}(F)$ splits over $F$ if there are scalars $c,a_1,...,a_n$ (not necessarily distinct) in $F$ such that

$$f(t)=c(t-a_1)(t-a_2)\cdots (t-a_n).$$

For example, $t^2-1=(t+1)(t-1)$ splits over $\mathbb{R}$, but $(t^2+1)(t-2)$ does not split over $\mathbb{R}$ because $t^2+1$ cannot be factored into a product of linear factors. However, $(t^2+1)(t-2)$ does split over $\mathbb{C}$ because it factors into the product $(t+i)(t-i)(t-2)$.

If $f(t)$ is the characteristic polynomial of a linear operator or a matrix over a field $F$, then the statement that $f(t)$ splits is understood to mean that it splits over $F$.

Theorem 5.6

The characteristic polynomial of any diagonalizable linear operator splits.

From this theorem, it is clear that if $\mathsf{T}$ is a diagonalizable linear operator on an $n$-dimensional vector space that fails to have distinct eigenvalues, then the characteristic polynomial of $\mathsf{T}$ must have repeated zeros.

The converse of Theorem 5.6 is false; that is, the characteristic polynomial of $\mathsf{T}$ may split, but $\mathsf{T}$ need not be diagonalizable. (See Example 5.2.3, which follows.) The following concept helps us determine when an operator whose characteristic polynomial splits is diagonalizable.

Definition: multiplicity

Let $\lambda$ be an eigenvalue of a linear operator or matrix with characteristic polynomial $f(t)$. The multiplicity (sometimes called the algebraic multiplicity) of $\lambda$ is the largest positive integer $k$ for which $(t-\lambda {)}^k$ is a factor of $f(t)$.

Example 5.2.2

Let

$$A=\left[\begin{array}{ccc}3& 1& 0\\ 0& 3& 4\\ 0& 0& 4\end{array}\right],$$

which has characteristic polynomial $f(t)=-(t-3{)}^2(t-4)$. Hence $\lambda =3$ is an eigenvalue of $A$ with multiplicity $2$, and $\lambda =4$ is an eigenvalue of $A$ with multiplicity $1$.

Remark

Let $A$ be a square matrix. A (complex) number $\lambda$ is an eigenvalue of $A$ if and only if $\lambda$ is a root of the characteristic equation of $A$.

The multiplicity of $\lambda$ being a root of the characteristic equation is called the algebraic multiplicity of $\lambda$, denoted $m_a$.

The dimension of the eigenspace associated to eigenvalue $\lambda$, that is, the maximum number of linearly independent eigenvectors associated with eigenvalue $\lambda$, is called the geometric multiplicity of $\lambda$, denoted $m_g$. It can be shown that for each eigenvalue $\lambda$, we have

$$1\le m_g\le m_a,$$

where $m_g$ and $m_a$ are the geometric and algebraic multiplicities of $\lambda$ respectively.

Therefore we have $A$ is diagonalizable if and only if the algebraic multiplicity and the geometric multiplicity are equal for all eigenvalues of $A$.

The eigenvectors of $\mathsf{T}$ corresponding to the eigenvalue $\lambda$ are the nonzero vectors in the null space of $\mathsf{T}-\lambda I$, we are led naturally to the study of this set.

eigenspace

Definition: eigenspace

Let $\mathsf{T}$ be a linear operator on a vector space $\mathsf{V}$ , and let $\lambda$ be an eigenvalue of $\mathsf{T}$ . Define ${\mathsf{E}}_{\lambda }=\{x\in \mathsf{V}:\mathsf{T}(x)=\lambda x\}=\mathsf{N}(\mathsf{T}-\lambda {\mathsf{I}}_{\mathsf{V}})$. The set ${\mathsf{E}}_{\lambda }$ is called the eigenspace of $\mathsf{T}$ corresponding to the eigenvalue $\lambda$. Analogously, we define the eigenspace of a square matrix $A$ corresponding to the eigenvalue $\lambda$ to be the eigenspace of ${\mathsf{L}}_A$ corresponding to $\lambda$.

Theorem 5.7

Let $\mathsf{T}$ be a linear operator on a finite-dimensional vector space $\mathsf{V}$, and let $\lambda$ be an eigenvalue of $\mathsf{T}$ having multiplicity $m$. Then

$$1\le \dim ({\mathsf{E}}_{\lambda })\le m,$$

where ${\mathsf{E}}_{\lambda }$ is the eigenspace corresponding to $\lambda$.

$$(1\le m_g\le m_a)$$

Example 5.2.3

Let $\mathsf{T}$ be the linear operator on ${\mathsf{P}}_2(\mathbb{R})$ defined by $\mathsf{T}(f(x))=f^{\prime }(x)$. The matrix representation of $\mathsf{T}$ with respect to the standard ordered basis $\beta$ for ${\mathsf{P}}_2(\mathbb{R})$ is

$$[\mathsf{T}{]}_{\beta }=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 2\\ 0& 0& 0\end{array}\right].$$

Consequently, the characteristic polynomial of $\mathsf{T}$ is

$$det([\mathsf{T}{]}_{\beta }-tI)=det\left[\begin{array}{ccc}-t& 1& 0\\ 0& -t& 2\\ 0& 0& -t\end{array}\right]=-t^3.$$

Thus $\mathsf{T}$ has only one eigenvalue ($\lambda =0$) with multiplicity $3$. Solving $\mathsf{T}(f(x))=f^{\prime }(x)=0$ shows that ${\mathsf{E}}_{\lambda }=N(\mathsf{T}-\lambda I)=N(\mathsf{T})$ is the subspace of ${\mathsf{P}}_2(\mathbb{R})$ consisting of the constant polynomials. So $\{1\}$ is a basis for ${\mathsf{E}}_{\lambda }$, and therefore $\dim ({\mathsf{E}}_{\lambda })=1$. Consequently, there is no basis for ${\mathsf{P}}_2(\mathbb{R})$ consisting of eigenvectors of $\mathsf{T}$, and therefore $\mathsf{T}$ is not diagonalizable.

A matrix is diagonalizable if and only if the algebraic multiplicity and geometric multiplicity are equal for all eigenvalues.

Example 5.2.4

Let $\mathsf{T}$ be the linear operator on ${\mathbb{R}}^3$ defined by

$$\mathsf{T}\left[\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right]=\left[\begin{array}{c}4a_1+a_3\\ 2a_1+3a_2+2a_3\\ a_1+4a_3\end{array}\right].$$

We determine the eigenspace of $\mathsf{T}$ corresponding to each eigenvalue. Let $\beta$ be the standard ordered basis for ${\mathbb{R}}^3$. Then

$$[\mathsf{T}{]}_{\beta }=\left[\begin{array}{ccc}4& 0& 1\\ 2& 3& 2\\ 1& 0& 4\end{array}\right],$$

and hence the characteristic polynomial of $\mathsf{T}$ is

$$det([\mathsf{T}{]}_{\beta }-tI)=det\left[\begin{array}{ccc}4-t& 0& 1\\ 2& 3-t& 2\\ 1& 4& a_3-t\end{array}\right]=-(t-5)(t-3{)}^2.$$

So the eigenvalues of $\mathsf{T}$ are ${\lambda }_1=5$ and ${\lambda }_2=3$ with multiplicities $1$ and $2$, respectively.

Since

$${\mathsf{E}}_{{\lambda }_1}=\mathsf{N}(\mathsf{T}-{\lambda }_{1}I)=\{\mathit{x}\in {\mathbb{R}}^3:(\mathsf{T}-5I)\mathit{x}=0\},$$

${\mathsf{E}}_{{\lambda }_1}$ is the solution space of the system of linear equations

$$\{\begin{array}{l}-x_1+x_3=0\\ 2x_1+2x_2+2x_3=0\\ x_1+x_3=0,\end{array}$$

which means ${\mathsf{E}}_{{\lambda }_1}$ is spanned by the basis $\{(1,2,-1)\}$. Hence, $\dim ({\mathsf{E}}_{{\lambda }_1})=1$.

Similarly, ${\mathsf{E}}_{{\lambda }_2}=\mathsf{N}(\mathsf{T}-3I)$ is the solution space of the system

$$\{\begin{array}{l}{x}_1+x_3=0\\ 2x_1+2x_3=0\\ x_1+x_3=0.\end{array}$$

Since the unknown $x_2$ does not appear in the first two equations, we assign it an arbitrary parameter $s$, and solve the system for $x_1$ and $x_3$, introducing another parameter $t$. The general solution to the system is

$$\mathit{x}=s\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right]+t\left[\begin{array}{c}-1\\ 0\\ 1\end{array}\right],\text{for some }x,t\in \mathbb{R}.$$

So a basis for ${\mathsf{E}}_{{\lambda }_2}$ is $\{(0,1,0),(-1,0,1)\}$ and $\dim ({\mathsf{E}}_{{\lambda }_2})=2$.

In this case, the multiplicity of each eigenvalue ${\lambda }_i$ is equal to the dimension of the corresponding eigenspace ${\mathsf{E}}_{{\lambda }_i}$. The union of the two bases just derived, namely,

$$\{(1,2,-1),(0,1,0),(-1,0,1)\},$$

is linearly independent and hence is a basis for ${\mathbb{R}}^3$ consisting of eigenvectors of $\mathsf{T}$. Consequently, $\mathsf{T}$ is diagonalizable.

Lemma

Let $\mathsf{T}$ be a linear operator, and let ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k$ be distinct eigenvalues of $\mathsf{T}$. For each $i=1,2,\dots ,k$, let $v_i\in {\mathsf{E}}_{{\lambda }_i}$, the eigenspace corresponding to ${\lambda }_i$. If

$$v_1+v_2+\cdots +v_k=0,$$

then $v_i=0$ for all $i$.

Theorem 5.5 says that eigenvectors which corresponds to different eigenvalues are linearly independent, so the only possibility is that they are all zeros.

Theorem 5.8

Let $\mathsf{T}$ be a linear operator on a vector space $\mathsf{V}$, and let ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k$ be distinct eigenvalues of $\mathsf{T}$. For each $i=1,\dots ,k$, let $S_i$ be a finite linearly independent subset of the eigenspace ${\mathsf{E}}_{{\lambda }_i}$. Then $S=S_1\cup S_2\cup \cdots \cup S_k$ is a linearly independent subset of $\mathsf{V}$.

Theorem 5.9

Let $\mathsf{T}$ be a linear operator on an $n$-dimensional vector space $\mathsf{V}$ such that the characteristic polynomial of $\mathsf{T}$ splits. Let ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k$ be the distinct eigenvalues of $\mathsf{T}$. Then

• $\mathsf{T}$ is diagonalizable if and only if the algebraic multiplicity of ${\lambda }_i$ equals $\dim ({\mathsf{E}}_{{\lambda }_i})$ for all $i$ (i.e. algebraic multiplicity = geometric multiplicity).
• If $\mathsf{T}$ is diagonalizable and ${\beta }_i$ is an ordered basis for ${\mathsf{E}}_{{\lambda }_i}$ for each $i$, then

$$\beta ={\beta }_1\cup {\beta }_2\cup \cdots \cup {\beta }_k$$

is an ordered basis for $V$ consisting of eigenvectors of $\mathsf{T}$.

Test for Diagonalizability

Let $\mathsf{T}$ be a linear operator on an $n$-dimensional vector space $V$. Then $\mathsf{T}$ is diagonalizable if and only if

1. The characteristic polynomial of $\mathsf{T}$ splits.
2. For each eigenvalue $\lambda$ of $\mathsf{T}$, the multiplicity of $\lambda$ equals the corresponding geometrical multiplicity:

$$\text{multiplicity}(\lambda )=\text{nullity}(\mathsf{T}-\lambda I)=n-\text{rank}(\mathsf{T}-\lambda I).$$

Example 5.2.5

We test the matrix

$$A=\left[\begin{array}{ccc}3& 1& 0\\ 0& 3& 0\\ 0& 0& 4\end{array}\right]\in {\mathsf{M}}_{3\times 3}(\mathbb{R})$$

for diagonalizability.

The characteristic polynomial of $A$ is

$$det(A-tI)=-(t-4)(t-3{)}^2,$$

which splits and so condition 1 of the test for diagonalization is satisfied. The eigenvalues are ${\lambda }_1=4$ and ${\lambda }_2=3$ with multiplicities $1$ and $2$, respectively.

Since ${\lambda }_1$ has multiplicity 1, condition 2 is satisfied for ${\lambda }_1$. For ${\lambda }_2$:

$$A-{\lambda }_{2}I=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]$$

the matrix $A-3I$ has rank 2, so the nullity is $3-2=1$, which is not the multiplicity of ${\lambda }_2$. Thus, condition 2 fails for ${\lambda }_2$ and $A$ is not diagonalizable.

Example 5.2.6 [core]

Let $\mathsf{T}$ be the linear operator on ${\mathsf{P}}_2(\mathbb{R})$ defined by

$$\mathsf{T}(f(x))=f(1)+f^{\prime }(0)x+(f^{\prime }(0)+f^{″}(0))x^2.$$

With $\alpha =\{1,x,x^2\}$ as the standard ordered basis for ${\mathsf{P}}_2(\mathbb{R})$, let $B=[\mathsf{T}{]}_{\alpha }$. Then

$$B=\left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 0& 1& 2\end{array}\right].$$

The characteristic polynomial of $B$, and hence of $\mathsf{T}$, is

$$-(t-1{)}^2(t-2),$$

which splits. Hence, condition 1 of the test for diagonalizability is satisfied.

Also, $B$ has eigenvalues ${\lambda }_1=1$ and ${\lambda }_2=2$ with multiplicities $2$ and $1$, respectively.

Condition 2 is satisfied for ${\lambda }_2$ because it has multiplicity $1$.

Checking condition 2 for ${\lambda }_1=1$:

$$\mathrm{rank}(B-{\lambda }_{1}I)=\mathrm{rank}\left(\begin{array}{ccc}0& 1& 1\\ 0& 0& 0\\ 0& 1& 1\end{array}\right)=1,$$

the rank of $B-I$ is 1, so nullity is $3-1=2$, which equals the multiplicity of ${\lambda }_1$. Therefore $\mathsf{T}$ is diagonalizable.

We now find an ordered basis $\gamma$ for ${\mathbb{R}}^3$ of eigenvectors of $B$. For each eigenvalue:

• The eigenspace corresponding to ${\lambda }_1=1$ is

$${\mathsf{E}}_{{\lambda }_1}=\{\mathit{x}\in {\mathbb{R}}^3:(B-I)\mathit{x}=0\}$$

which is the solution space for the system

$$x_2+x_3=0,$$

and has

$${\gamma }_1=\{\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right],\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right]\}.$$

as a basis.

• The eigenspace corresponding to ${\lambda }_2=2$ is

$${\mathsf{E}}_{{\lambda }_2}=\{\mathit{x}\in {\mathbb{R}}^3:(B-2I)\mathit{x}=0\}$$

which is the solution space for the system

$$\begin{array}{rlrl}-x_1+& x_2+x_3& & =0\\ & x_2& & =0,\end{array}$$

and has

$${\gamma }_1=\left\{\left[\begin{array}{c}1\\ 0\\ 1\end{array}\right]\right\}.$$

as a basis.

Let

$$\gamma ={\gamma }_1\cup {\gamma }_2=\{\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right],\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right],\left[\begin{array}{c}1\\ 0\\ 1\end{array}\right]\}$$

Then $\gamma$ is an ordered basis for ${\mathbb{R}}^3$ consisting of eigenvectors of$B$.

Finally, observe that the vector in $\gamma$ are the coordinatevectors relative to $\alpha$ of the vectors in the set

$$\beta =\{1,-x+x^2,1+x^2\},$$

which is an ordered basis for ${\mathsf{P}}_2(\mathbb{R})$ consisting of eigenvectors of $\mathsf{T}$. Thus

$$[\mathsf{T}{]}_{\beta }=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 2\end{array}\right].$$

Example 5.2.7

Let

$$A=\left[\begin{array}{cc}0& -2\\ 1& 3\end{array}\right].$$

We show $A$ is diagonalizable and find a $2\times 2$ matrix $Q$ such that $Q^{-1}AQ$ is diagonal. We then show how to use this result to compute $A^n$ for any positive integar $n$.

First observe the characteristic polynomial of $A$ is $(t-1)(t-2)$, so $A$ has two distinct eigenvalues, ${\lambda }_1=1$ and ${\lambda }_2=2$.

By applying the corollary to Theorem 5.5 to the operator ${\mathsf{L}}_A$, $A$ is diagonalizable. Moreover,

$${\gamma }_1=\{(-2,1{)}^{\mathrm{\top }}\},{\gamma }_2=\{(-1,1{)}^{\mathrm{\top }}\}.$$

are bases for the eigenspaces ${\mathfrak{E}}_{{\lambda }_1}$ and ${\mathfrak{E}}_{{\lambda }_2}$, respectively. Therefore,

$$\gamma ={\gamma }_1\cup {\gamma }_2=\{(-2,1{)}^{\mathrm{\top }},(-1,1{)}^{\mathrm{\top }}\}$$

is an ordered basis for ${\mathbb{R}}^2$ consisting of eigenvectors of ${\mathbb{R}}^2$. Let

$$Q=\left[\begin{array}{cc}-2& -1\\ 1& 1\end{array}\right]$$

be the matrix whose columns are the vectors in $\gamma$. Then, by the corollary to Theorem 2.23,

$$D=Q^{-1}AQ=\left[\begin{array}{cc}1& 0\\ 0& 2\end{array}\right].$$

To compute $A^n$ for any positive integer $n$,

$$\begin{array}{rl}{A}^n& =(QD{Q}^{-1}{)}^n=(QD{Q}^{-1})(QD{Q}^{-1})\cdots (QD{Q}^{-1})\\ & =Q{D}^n{Q}^{-1}\\ & =Q\left[\begin{array}{cc}{1}^n& 0\\ 0& 2^n\end{array}\right]Q^{-1}\\ & =\left[\begin{array}{cc}-2& -1\\ 1& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 2^n\end{array}\right]\left[\begin{array}{cc}-1& -1\\ 1& 2\end{array}\right]=\left[\begin{array}{cc}2-2^n& 2-2^{n+1}\\ -1+2^n& -1+2^{n+1}\end{array}\right].\end{array}$$

Systems of Differential Equations

Exercise 5.2.8

Consider the system of differential equations

$$\{\begin{array}{l}{x}_1^{\prime }=3x_1+x_2+x_3\\ x_2^{\prime }=2x_1+4x_2+2x_3\\ x_3^{\prime }=-x_1-x_2+x_3,\end{array}$$

where each $x_i=x_i(t)$ is a differentiable real-valued function of the real value $t$. Clearly, this system has a solution, namel, the solution in which each $x_i(t)$ is the zero function. We determine all of the solutions to this system.

Let $x:\mathbb{R}\to {\mathbb{R}}^3$ be

$$\mathit{x}(t)=\left[\begin{array}{c}{x}_1(t)\\ x_2(t)\\ x_3(t)\end{array}\right],$$

and ${\mathit{x}}^{\prime }(t)$ is the derivative of $\mathit{x}$.

Let

$$A=\left[\begin{array}{ccc}3& 1& 1\\ 2& 4& 2\\ -1& -1& 1\end{array}\right].$$

be the coefficient omatrix of the given system, so that we can rewrite the system as matrix equation ${\mathit{x}}^{\prime }=A\mathit{x}$.

It can be verified that for

$$Q=\left[\begin{array}{ccc}-1& 0& -1\\ 0& -1& -2\\ 1& 1& 1\end{array}\right]\text{and}D=\left[\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 4\end{array}\right],$$

we have $Q^{-1}AQ=D$. Substitute $A=QD{Q}^{-1}$ into ${\mathit{x}}^{\prime }=A\mathit{x}$ to obtain

$${\mathit{x}}^{\prime }=QD{Q}^{-1}\mathit{x},$$

or equivalently,

$$Q^{-1}{\mathit{x}}^{\prime }=D{Q}^{-1}\mathit{x}.$$

Define $\mathit{y}(t)=Q^{-1}\mathit{x}(t)$ yielding ${\mathit{y}}^{\prime }=Q^{-1}{\mathit{x}}^{\prime }$. Hence,

$${\mathit{y}}^{\prime }=D\mathit{y},$$

which is a system of decoupled equations

$$\{\begin{array}{l}{y}_1^{\prime }=2y_1\\ y_2^{\prime }=2y_2\\ y_3^{\prime }=4y_3.\end{array}$$

Solutions for each $y_i$ are

$$y_1(t)=c_1{e}^{2t},y_2(t)=c_2{e}^{2t},y_3(t)=c_3{e}^{4t},$$

with arbitrary constants $c_1,c_2,c_3$.

Back-substituting,

$$\begin{array}{rl}& \mathit{x}(t)=Q\mathit{y}(t)=\left[\begin{array}{ccc}-1& 0& -1\\ 0& -1& -2\\ 1& 1& 1\end{array}\right]\left[\begin{array}{c}{c}_1{e}^{2t}\\ c_2{e}^{2t}\\ c_3{e}^{4t}\end{array}\right]\\ =& \left[\begin{array}{c}{c}_1{e}^{2t}+c_3{e}^{4t}\\ -c_2{e}^{2t}-c_3{e}^{4t}\\ c_1{e}^{2t}+c_2{e}^{2t}+c_3{e}^{4t}\end{array}\right].\end{array}$$

Thus the general solution is

$$\begin{array}{rl}\mathit{x}(t)& =e^{2t}{z}_1+e^{4t}{z}_2\\ & =e^{2t}[c_1\left[\begin{array}{c}-1\\ 0\\ 1\end{array}\right]+c_2\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right]]=e^{4t}\left[c_3\left[\begin{array}{c}-1\\ -2\\ 1\end{array}\right]\right].\end{array}$$

where $z_1\in {\mathsf{E}}_{{\lambda }_1}$ and $z_2\in {\mathsf{E}}_{{\lambda }_2}$, with ${\lambda }_1=2$ and ${\lambda }_2=4$.

This concludes the main part of the example.

Here is more generalized conclusion.

Application for ODE

Let $n\times n$ matrix $A=(a_{ij})$ be the coefficient matrix of a system of differential equations

$$x_i^{\prime }=\sum _{j=1}^n{a}_{ij}{x}_j,i=1,\dots ,n.$$

Suppose $A$ is diagonalizable and the distinct eigenvalues of $A$ are ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_k$.

Prove that a differentiable function $x:\mathbb{R}\to {\mathbb{R}}^n$ is a solution to the system if and only if

$$x(t)=e^{{\lambda }_{1}t}{z}_1+e^{{\lambda }_{2}t}{z}_2+\cdots +e^{{\lambda }_{k}t}{z}_k,$$

where $z_i\in {\mathsf{E}}_{{\lambda }_i}$ for $i=1,\dots ,k$. Use this result to prove that the set of solutions form an $n$-dimensional real vector space.

Following the step of the previous exercise, we may pick a matrix $Q$ whose column vectors consist of eigenvectors and $Q$ is invertible. Let $D$ be the diagonal matrix $Q^{-1}AQ$. And we also know that finally we'll have the solution $x=Qu$ for some vector $u$ whose $i$-th entry is $c_i{e}^{\lambda }$ if the $i$-th column of $Q$ is an eigenvector corresponding to $\lambda$. By denoting $\overline{D}$ to be the diagonal matrix with ${\overline{D}}_{ii}=e^{D_{ii}}$, we may write $x=Q\overline{D}y$. where the $i$-th entry of $y$ is $c_i$. So the solution must be of the form described in the exercise.

For the second statement, we should know first that the set

$$\{e^{{\lambda }_{1}t},e^{{\lambda }_{2}t},\dots e^{{\lambda }_{k}t}\}$$

are linearly independent in the space of real functions. Since $Q$ invertible, we know that the solution set

$$\{Q\overline{D}y:y\in {\mathbb{R}}^n\}$$

is an $n$-dimensional real vector space.