Laplace Transform

• Formulation & Definition
• Properties
• Inversion of Laplace Transform

Formulation & Definition

Introduction

In mathematics, the Laplace transform, named after its inventor Pierre-Simon Laplace is an integral transform that converts a function of a real variable $t$ (often time) to a function of a complex variable $s$ (complex frequency).

For suitable functions $f$, the Laplace transform is the integral

$$\mathcal{L}\{f\}(s)={\int }_0^{\mathrm{\infty }}f(t)e^{-st}\mathrm{d}t.$$

Here's the Fourier Transformation (for real number):

$$\mathcal{F}(\omega )=\mathcal{F}(f(t))={\int }_0^{\mathrm{\infty }}f(t)e^{-i\omega t}\mathrm{d}t.$$

Why do we need Laplace Transform for solving ODE?

The Formulation of Laplace Transform

Definition: Laplace Transform

If a function $f(t)$ is multiplied by $e^{-st}$, and the result is integrated with respect to $t$ from $t=0$ to $t=\mathrm{\infty }$, a new function of the variable $s$ is obtained when the integral exists.

This function (when it exists) is called the Laplace transform of $f(t)$:

$$\mathcal{L}\{f\}(s)={\int }_0^{\mathrm{\infty }}f(t)e^{-st}\mathrm{d}t.$$

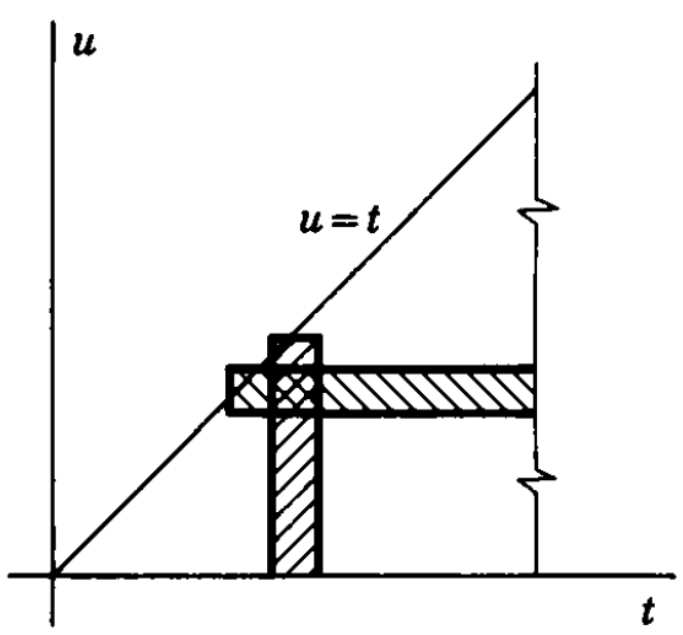
Suppose that we require the solution of the differential equation:

$$\frac{\mathrm{d}y}{\mathrm{d}t}-y=e^{at}$$

for positive values of $t$, which satisfies the initial condition

$$y(0)=-1.$$

$$\begin{array}{rl}& \frac{\mathrm{d}y}{\mathrm{d}t}-y=e^{at}\\ ⟹& \text{Let}p=\exp (\int -1\mathrm{d}t)=\exp (-t)\\ ⟹& y=\frac{1}{p}\int p{e}^{at}\mathrm{d}t+\frac{c}{\exp (-t)}\\ & y=\exp (t)\int \exp (-t+at)\mathrm{d}t+c\exp (t)\\ & y=\exp (t)(c+\frac{1}{a-1}\exp ((a-1)t))\\ y(0)=-1⟹& c=-1-\frac{1}{a-1}=-\frac{a}{a-1}\\ ⟹& y=\exp (t)(-\frac{a}{a-1}+\frac{1}{a-1}\exp ((a-1)t))\\ & y=\frac{1}{a-1}(\exp (at)-a\exp (t))\end{array}$$

1. We first take the Laplace transform of both sides of the previous equation, by multiplying both sides of the equation by $e^{-st}$ and integrating the results with respect to $t$ from zero to infinity,

$${\int }_0^{\mathrm{\infty }}{e}^{-st}\frac{\mathrm{d}y}{\mathrm{d}t}\mathrm{d}t-{\int }_0^{\mathrm{\infty }}{e}^{-st}y\mathrm{d}t={\int }_0^{\mathrm{\infty }}{e}^{-st}{e}^{at}\mathrm{d}t$$

2. The integral on the right is readily evaluated

$${\int }_0^{\mathrm{\infty }}{e}^{-st}{e}^{at}\mathrm{d}t=-{\frac{e^{-(s-a)t}}{s-a}|}_0^{\mathrm{\infty }}=\frac{1}{s-a}$$

the integral exists when $s>a$. The first integral on the left can be integrated formally by parts to give

$$\begin{array}{rl}{\int }_0^{\mathrm{\infty }}{e}^{-st}\frac{\mathrm{d}y}{\mathrm{d}t}\mathrm{d}t& ={e^{-st}y(t)|}_0^{\mathrm{\infty }}+s{\int }_0^{\mathrm{\infty }}{e}^{-st}y\mathrm{d}t\\ & =-y(0)+s{\int }_0^{\mathrm{\infty }}{e}^{-st}y\mathrm{d}t\\ & =1+s{\int }_0^{\mathrm{\infty }}{e}^{-st}y\mathrm{d}t\end{array}$$

1. As a result, we obtain

$$\begin{array}{rl}& (s-1){\int }_0^{\mathrm{\infty }}{e}^{-st}y\mathrm{d}t=\frac{1}{s-a}-1\text{ or }\\ & {\int }_0^{\mathrm{\infty }}{e}^{-st}y\mathrm{d}t=\frac{a+1-s}{(s-1)(s-a)}\end{array}$$

1. Expand this expression by the method of partial fractions, to obtain the equivalent form

$${\int }_0^{\mathrm{\infty }}{e}^{-st}y\mathrm{d}t=\frac{1}{a-1}\frac{1}{s-a}-\frac{a}{a-1}\frac{1}{s-1}$$

1. Reference to ${\int }_0^{\mathrm{\infty }}{e}^{-t}{e}^{at}\mathrm{d}t=-{\frac{e^{-(-b-a)t}}{s-a}|}_0^{\mathrm{\infty }}=\frac{1}{s-a}$, then indicates that, since $1/(s-a)$ is the transform of $e^{at}$, the first term is the transform of $e^{at/(a-1)}$ and the second term the transform of $-{ae}^t/(a-1)$.

2. The original problem is now apparently reduced to the problem of determining a function $y(t)$ whose Laplace transform is given by the above equation

3. Applying the inverse Laplace transform, one can obtain for $a\ne 1$

$$y=\frac{1}{a-1}(e^{at}-a{e}^t)$$

or for $a=1$, can be obtained by taking the limit as $a\to 1$

$$y=(t-1)e^t$$

Definition of Laplace Transform

The Laplace transform of a function $f(t)$, defined for positive values of $t$, is frequently indicated by the notation $\mathcal{L}\{f(t)\}$ and is defined, as a function of the variable $s$, by the integral

$$\mathcal{L}\{f(t)\}={\int }_0^{\mathrm{\infty }}f(t)e^{-st}\mathrm{d}t.$$

over that range of values of $s$ for which the integral exists.

The notation $\overline{f}(s)$ or merely $\overline{f}$ is also used in place of $\mathcal{L}\{f(t)\}$.

The Existence of Laplace Transform

• Integration may fail to define a function of $s$, in particular, because of infinite discontinuities in $f(t)$ for certain positive values of $t$ or because of failure of $f(t)$ to behave in a sufficiently regular way near $t=0$ or for large values of $t$. However, the presence of a finite number of finite discontinuities or "jumps" will not, in itself, affect the existence of the integral
• A function $f(t)$ is said to be piecewise continuous in a finite range if it is possible to divide that range into a finite number of intervals such that $f(t)$ is continuous inside each interval and approaches finite values as either end of any interval is approached from the interior. Such functions may thus have finite jumps at points inside the range considered

$$\mathcal{L}\{f(t)\}={\int }_0^{\mathrm{\infty }}f(t)e^{-st}\mathrm{d}t=({\int }_0^{t_1}+{\int }_{t_1}^T+{\int }_T^{\mathrm{\infty }})f(t)e^{-st}\mathrm{d}t$$

Sufficient additional condition to guarantee the existence of the third integral item $\mathcal{L}\{f(t)\}={\int }_T^{\mathrm{\infty }}f(t)e^{-st}\mathrm{d}t$, at least for sufficiently large values of $s$, is the requirement that $f(t)$ belong to the rather extensive class of "functions of exponential order".

A function $f(t)$ is said to be of exponential order if, for some number $s_0$, the product $e^{-s_{0}t}|f(t)|$ is bounded for large values of $t$, say for $t>T$.

If the bound is denoted by $M$, then there follows, when $t>T$:

$$\begin{gathered} e^{-s_{0}t}|f(t)|<M,\text{ or }|f(t)|<M{e}^{s_{0}t}. \\ ⟹|e^{-st}f(t)|<e^{-st}\cdot M{e}^{s_{0}t}=M{e}^{-(s-s_0)t} \end{gathered}$$

the Laplace transform of $f(t)$ exists, when $s$ is sufficiently large, if $f(t)$ satisfies the following conditions:

• $f(t)$ is continuous or piecewise continuous in every finite interval $t_1\le t\le T$, where $t_1>0$.
• $t^n|f(t)|$ is bounded near $t=0$ for some number $n$, where $n<1$.
• $e^{-s_{0}t}|f(t)|$ is bounded for large values of $t$, for some number $s_0$.

Examples for Laplace Transforms

$$\begin{array}{rl}\mathcal{L}\{1\}& ={\int }_0^{\mathrm{\infty }}{e}^{-st}dt=-{\frac{e^{-st}}{s}|}_0^{\mathrm{\infty }}=\frac{1}{s}(s>0).\\ \mathcal{L}\left\{e^{at}\right\}& ={\int }_0^{\mathrm{\infty }}{e}^{-(s-a)t}dt=-{\frac{e^{-(s-a)t}}{s-a}|}_0^{\mathrm{\infty }}=\frac{1}{s-a}(s>a).\\ \mathcal{L}\{\sin at\}& ={\int }_0^{\mathrm{\infty }}{e}^{-st}\sin atdt=-{\frac{e^{-st}}{s^2+a^2}(s\sin at+a\cos at)|}_0^{\mathrm{\infty }}\\ & =\frac{a}{s^2+a^2}(s>0).\end{array}$$

Properties

Properties of Laplace Transform

Some most useful properties of Laplace transforms:

$$\mathcal{L}\{af(t)+bg(t)\}=a\overline{f}(s)+b\overline{g}(s)$$$$\begin{array}{rl}\mathcal{L}\left\{\frac{{\mathrm{d}}^{n}f(t)}{\mathrm{d}{t}^n}\right\}=& s^n\overline{f}(s)-[s^{n-1}f(0+)+s^{n-2}\frac{\mathrm{d}f(0+)}{\mathrm{d}t}\\ & +s^{n-3}\frac{{\mathrm{d}}^{2}f(0+)}{\mathrm{d}{t}^2}+\cdots +\frac{{\mathrm{d}}^{n-1}f(0+)}{\mathrm{d}{t}^{n-1}}]\end{array}$$

$$\mathcal{L}\left\{\frac{\mathrm{d}f(t)}{\mathrm{d}t}\right\}={\int }_0^{\mathrm{\infty }}{e}^{-st}\frac{\mathrm{d}f(t)}{\mathrm{d}t}\mathrm{d}t$$

An integration by parts gives

$${\int }_0^{\mathrm{\infty }}{e}^{-st}\frac{\mathrm{d}f(t)}{\mathrm{d}t}\mathrm{d}t={e^{-st}f(t)|}_0^{\mathrm{\infty }}+s{\int }_0^{\mathrm{\infty }}{e}^{-st}f(t)\mathrm{d}t$$

if $f(t)$ is continuous and $\frac{\mathrm{d}f(t)}{\mathrm{d}t}$ is piecewise continuous in every interval But since $f(t)$ is of exponential order, the integrated part vanishes as (for $s>s_0$ ), and there follows

$$\begin{array}{rl}\mathcal{L}\left\{\frac{\mathrm{d}f(t)}{\mathrm{d}t}\right\}=& s\overline{f}(s)-f(0+)\\ \mathcal{L}\left\{\frac{{\mathrm{d}}^{2}f(t)}{\mathrm{d}{t}^2}\right\}=& {\int }_0^{\mathrm{\infty }}{e}^{-st}\frac{{\mathrm{d}}^{2}f(t)}{\mathrm{d}{t}^2}\mathrm{d}t\\ =& {e^{-st}\frac{\mathrm{d}f(t)}{\mathrm{d}t}|}_0^{\mathrm{\infty }}+s{\int }_0^{\mathrm{\infty }}{e}^{-st}\frac{\mathrm{d}f(t)}{\mathrm{d}t}\mathrm{d}t\\ =& {e^{-st}\frac{\mathrm{d}f(t)}{\mathrm{d}t}|}_0^{\mathrm{\infty }}+s\mathcal{L}\left\{\frac{\mathrm{d}f(t)}{\mathrm{d}t}\right\}\\ \mathcal{L}\left\{\frac{{\mathrm{d}}^{2}f(t)}{\mathrm{d}{t}^2}\right\}=& s^2\overline{f}(s)-sf(0+)-\frac{\mathrm{d}f(0+)}{\mathrm{d}t}\end{array}$$

$$\mathcal{L}\{{\int }_0^{t}f(u)\mathrm{d}u\}=\frac{1}{s}\overline{f}(s)$$

$$\begin{array}{rl}\mathcal{L}\{{\int }_0^{t}f(u)\mathrm{d}u\}& ={\int }_0^{\mathrm{\infty }}{e}^{-st}\{{\int }_0^{t}f(u)\mathrm{d}u\}\mathrm{d}t\\ & ={[\frac{e^{-st}}{-s}{\int }_0^{t}f(u)\mathrm{d}u]}_0^{\mathrm{\infty }}+\frac{1}{s}{\int }_0^{\mathrm{\infty }}{e}^{-st}f(t)\mathrm{d}t\\ & =\frac{1}{s}\overline{f}(s)\end{array}$$

the integrated part vanishing at the upper limit (for sufficiently large values of $s$ ), since $f(t)$, and hence ${\int }_0^{t}f(u)\mathrm{d}u$, is of exponential order. Thus, in general, if a function is integrated over $(0,t)$, the transform of the integral is obtained by dividing the transform of the function by $s$.

If the lower limit differs from zero, the formula

$$\mathcal{L}\{{\int }_a^{t}f(u)\mathrm{d}u\}=\frac{1}{s}\overline{f}(s)-\frac{1}{s}{\int }_0^{a}f(u)\mathrm{d}u$$

is easily established.

$$\mathcal{L}\{e^{at}f(t)\}=\overline{f}(s-a)$$

If $f(t)=\left\{\begin{array}{cc}0,& t<a\\ g(t-a),& t\geqq a\end{array}\right\}$ with $a\geqq 0$, then $\overline{f}(s)=e^{-as}\overline{g}(s)$.

$$\mathcal{L}\{t^{n}f(t)\}=(-1{)}^n\frac{{\mathrm{d}}^n\overline{f}(s)}{\mathrm{d}{s}^n}$$$$\mathcal{L}\{{\int }_0^{t}f(t-u)g(u)\mathrm{d}u\}=\overline{f}(s)\overline{g}(s)$$

In these equations $a$ and $b$ are constants, and $n$ is a positive integer.

The Convolution Properity

$$\begin{array}{c}\mathcal{L}\{{\int }_0^{t}f(t-u)g(u)\mathrm{d}u\}=\overline{f}(s)\overline{g}(s)\\ \begin{array}{rl}\overline{f}(s)\overline{g}(s)=& [{\int }_0^{\mathrm{\infty }}{e}^{-sv}f(v)\mathrm{d}v][{\int }_0^{\mathrm{\infty }}{e}^{-su}g(u)\mathrm{d}u]\\ =& {\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}{e}^{-s(v+u)}f(v)g(u)\mathrm{d}v\mathrm{d}u\\ =& {\int }_0^{\mathrm{\infty }}g(u)\{{\int }_0^{\mathrm{\infty }}{e}^{-s(v+u)}f(v)\mathrm{d}v\}\mathrm{d}u\end{array}\end{array}$$

if different "dummy variables" of integration ( $v$ and $u$ ) are used in defining the two transforms. If, in the inner integral of the last form, we replace $v$ by a new variable $t$ with the substitution

$$v=t-u,\mathrm{d}v=\mathrm{d}t,$$

there follows

$${\int }_0^{\mathrm{\infty }}{e}^{-s(v+u)}f(v)\mathrm{d}v={\int }_u^{\mathrm{\infty }}{e}^{-st}f(t-u)\mathrm{d}t$$

and hence

$$\begin{array}{rl}\overline{f}(s)\overline{g}(s)& ={\int }_0^{\mathrm{\infty }}g(u)\{{\int }_u^{\mathrm{\infty }}{e}^{-st}f(t-u)\mathrm{d}t\}\mathrm{d}u\\ & ={\int }_0^{\mathrm{\infty }}{e}^{-st}\{{\int }_0^{t}f(t-u)g(u)\mathrm{d}u\}\mathrm{d}t\\ & =\mathcal{L}\{{\int }_0^{t}f(t-u)g(u)\mathrm{d}u\}.\end{array}$$

Inversion of Laplace Transform

Inverse of the Laplace Transform

To determine the inverse transform of a given function $F(s)$ it is thus necessary to determine a function $f(t)$ which satisfies the equation

$${\int }_0^{\mathrm{\infty }}{e}^{-st}f(t)\mathrm{d}t=F(s).⟺f(t)={\mathcal{L}}^{-1}\{F(s)\}.$$

Since the unknown function $f(t)$ appears under an integral sign, an equation of this type is called an integral equation.

In more advanced works it is proved that if this equation has a solution, then that solution is unique. Thus, if one function having a given transform is known, it is the only possible one. This result is known as Lerch's theorem.

More precisely, Lerch's theorem states that two functions having the same transform cannot differ throughout any interval of positive length. Thus, for example, it's shown that the continuous solution of

$${\int }_0^{\mathrm{\infty }}{e}^{-st}f(t)\mathrm{d}t=\frac{1}{s}$$

is $f(t)=1$; that is, ${\mathcal{L}}^{-1}\left\{s^{-1}\right\}=1$. However, it is clear that if we take $f(t)$ to be, say, zero at $t=1$ and unity elsewhere, or otherwise redefine the function $f(t)$ at a finite number of points, the value of the integral is not changed. Hence the new function is also a solution. Such artificialities are, however, generally of no significance in applications.

Table: Laplace Transform

	Transform	Function
T1	$\overline{f}(s)=\mathcal{L}\{f(t)\}={\int }_0^{\mathrm{\infty }}{e}^{-st}f(t)\mathrm{d}t$	$f(t)$
T2	$a\overline{f}(s)+b\overline{g}(s)$	$af(t)+bg(t)$
T3	$s\overline{f}(s)-f(0)$	$\frac{\mathrm{d}f(t)}{\mathrm{d}t}$
T4	$s^2\overline{f}(s)-sf(0)-\frac{\mathrm{d}f(0)}{\mathrm{d}t}$	$\frac{{\mathrm{d}}^{2}f(t)}{\mathrm{d}{t}^2}$
T5	$s^n\overline{f}(s)-\sum _{k=1}^n{s}^{n-k}\frac{{\mathrm{d}}^{k-1}f(0)}{\mathrm{d}{t}^{k-1}}$	$\frac{{\mathrm{d}}^{n}f(t)}{\mathrm{d}{t}^n}$
T6	$\frac{1}{s^n}\overline{f}(s)$	$\stackrel{n\text{ times }}{\overbrace{{\int }_0^t\cdots {\int }_0^t}}f(t)\stackrel{n\text{ times }}{\overbrace{\mathrm{d}t\cdots \mathrm{d}t}}$
T7	$(-1{)}^n\frac{{\mathrm{d}}^n\overline{f}(s)}{\mathrm{d}{s}^n}$	$t^{n}f(t)$
T8	$\overline{f}(s-a)$	$e^{at}f(t)$
T9	$e^{-as}\overline{f}(s)$	$\{\begin{array}{c}f(t-a)\\ 0\end{array}$
T10	$\overline{f}(s)\overline{g}(s)$	${\int }_0^{t}f(t-u)g(u)\mathrm{d}u={\int }_0^{t}f(u)g(t-u)\mathrm{d}u$
T11	$\frac{1}{s}$	1
T12	$\frac{1}{s+a}$	$e^{-at}$
T13	$\frac{1}{(s+a)(s+b)}$	$\frac{1}{a-b}(e^{-bt}-e^{-at})$
T14	$\frac{s}{(s+a)(s+b)}$	$\frac{1}{b-a}(b{e}^{-bt}-a{e}^{-at})$
T15	$\frac{a}{s^2+a^2}$	$\sin at$
T16	$\frac{s}{s^2+a^2}$	$\cos at$
T17	$\frac{a}{s^2-a^2}$	$\sinh at$
T18	$\frac{s}{s^2-a^2}$	$\cosh at$
T19	$\frac{2as}{{(s^2+a^2)}^2}$	$t\sin at$
T20	$\frac{s^2-a^2}{{(s^2+a^2)}^2}$	$t\cos at$
T21	$\frac{2a^3}{{(s^2+a^2)}^2}$	$\sin at-at\cos at$
T22	$\frac{2as}{{(s^2-a^2)}^2}$	$t\sinh at$
T23	$\frac{s^2+a^2}{{(s^2-a^2)}^2}$	$t\cosh at$
T24	$\frac{2a^3}{{(s^2-a^2)}^2}$	$at\cosh at-\sinh at$
T25	$\frac{a}{(s+b{)}^2+a^2}$	$e^{-bt}\sin at$
T26	$\frac{s+b}{(s+b{)}^2+a^2}$	$e^{-bt}\cos at$
T27	$\frac{4c^3}{s^4+4a^4}$	$\sin at\cosh at-\cos at\sinh at$
T28	$\frac{2a^{2}s}{s^4+4a^1}$	$\sin at\sinh at$
T29	$\frac{2a^3}{s^4-a^4}$	$\sinh at-\sin at$
T30	$\frac{2a^{1}s}{s^4-a^4}$	$\cosh at-\cos at$
T31	1	$\delta (t)$
T32	$e^{-s{t}_1}$	$\delta (t-t_1)$
T33	$s$	${\delta }^{\prime }(t)$
T34	$s{e}^{-s{t}_1}$	${\delta }^{\prime }(t-t_1)$
T35	$\frac{1}{s^n}$	$\frac{t^{n-1}}{(n-1)!}$
T35a	$\frac{n!}{s^{n+1}}$	$t^n$
T36	$\frac{1}{(s+a{)}^n}$	$\frac{t^{\mathrm{a}-1}{e}^{-at}}{(n-1)!}$
T37	$\frac{s}{(s+a{)}^n}$	$\frac{(n-1)-at}{(n-1)!}{t}^{n-2}{e}^{-at}$
T38	$\frac{a^{2n-1}}{{(s^2+a^2)}^n}$	$\frac{1}{2^{n-1}(n-1)!}[\sqrt{\frac{\pi }{2}}(at{)}^{n-1/2}{J}_{n-1/2}(at)](n>0)$
T39	$\frac{a^{2n-2}s}{{(s^2+a^2)}^n}$	$\frac{at}{2^n(n-1)!}[\sqrt{\frac{\pi }{2}}(at{)}^{n-3/2}{J}_{n-3/2}(at)](n>\frac{1}{2})$
T40	$\frac{a^{2n-1}}{{(s^2-a^2)}^n}$	$\frac{1}{2^{n-1}(n-1)!}[\sqrt{\frac{\pi }{2}}(at{)}^{n-1/2}{I}_{n-1/2}(at)](n>0)$
T41	$\frac{a^{2n-2}s}{{(s^2-a^2)}^n}$	$\frac{at}{2^n(n-1)!}[\sqrt{\frac{\pi }{2}}(at{)}^{n-3/2}{I}_{n-3/2}(at)](n>\frac{1}{2})$

Table: Bessel functions of order half an odd integer

$m$	$\sqrt{\frac{\pi }{2}}{x}^m{J}_m(x)$	$\sqrt{\frac{\pi }{2}}{x}^m{I}_m(x)$
-1/2	$(\cos x)/x$	$(\cosh x)/x$
$\frac{1}{2}$	$\sin x$	$\sinh x$
$\frac{3}{2}$	$\sin x-x\cos x$	$x\cosh x-\sinh x$
$\frac{5}{2}$	$(3-x^x)\sin x-3x\cos x$	$(3+x^2)\sinh x-3x\cosh x$
7/2	$(15-6x^2)\sin x-(15-x^2)x\cos x$	$(15+x^2)x\cosh x-(15+6x^2)\sinh x$
$\frac{9}{2}$	$(105-45x^2+1)\sin x-(105-10x^2)x\cos x$	$(105+45x^2+1)\sinh x-(105+10x^2)x\cosh x$
	Recurrence Formulas
	$x^{m+1}{J}_{m+1}(x)=2m[x^m{J}_m(x)]-x^2[x^{m-1}{J}_{m-1}(x)]$	$x^{m+1}{I}_{m+1}(x)=-2m[x^m{I}_m(x)]+x^2[x^{m-1}{I}_{m-1}(x)]$

Method of Partial Fractions for the Inverse of Laplace Transform

For

$$F(s)=\frac{N(s)}{D(s)}$$

where $D(s)$ is a polynomial of degree $n$ with $n$ distinct real zeros $s=a_1,a_2$, $a_n$, and $N(s)$ is a polynomial of degree $n-1$ or less, there follows

$$\begin{array}{rl}\frac{N(s)}{D(s)}& =\frac{N\left(a_1\right)}{D^{\prime }\left(a_1\right)}\frac{1}{s-a_1}+\frac{N\left(a_2\right)}{D^{\prime }\left(a_2\right)}\frac{1}{s-a_2}+\cdots +\frac{N\left(a_n\right)}{D^{\prime }\left(a_n\right)}\frac{1}{s-a_n}\\ & =\sum _{m=1}^n\frac{N\left(a_m\right)}{D^{\prime }\left(a_m\right)}\frac{1}{s-a_m}\end{array}$$

(Heaviside cover-up method / Residue Method)Let

$$\begin{array}{rl}& \frac{N(s)}{D(s)}=\sum _{m=1}^n\frac{A_m}{s-a_m}\\ ⟹& (s-a_k)\frac{N(s)}{D(s)}=A_k+\sum _{m=1,m\ne k}^n{A}_m\frac{s-a_k}{s-a_m}\\ ⟹& \underset{s\to a_k}{lim}(s-a_k)\frac{N(s)}{D(s)}=\underset{s\to a_k}{lim}(A_k+\sum _{m=1,m\ne k}^n{A}_m\frac{s-a_k}{s-a_m})\\ & \underset{s\to a_k}{lim}\frac{N(s)}{\frac{D(s)-D(a_k)}{s-a_k}}=A_k\\ ⟹& \frac{N(a_k)}{D^{\prime }(a_k)}=A_k.\end{array}$$

and hence, from (T12),

$${\mathcal{L}}^{-1}\left\{\frac{N(s)}{D(s)}\right\}=\sum _{m=1}^n\frac{N\left(a_m\right)}{D^{\prime }\left(a_m\right)}{e}^{a_{m}t}$$

Example1: Inverse Laplace Transform

To determine ${\mathcal{L}}^{-1}\left\{\frac{s^2+1}{s^3+3s^2+2s}\right\}$, we write

$$N(s)=s^2+1,D(s)=s^3+3s^2+2s=s(s+1)(s+2)$$

With $a_1=0,a_2=-1,a_3=-2$, and $D^{\prime }=3s^2+6s+2$, there follows

$$\begin{array}{c}\begin{array}{cl}N\left(a_1\right)=1,& D^{\prime }\left(a_1\right)=2,\\ N\left(a_2\right)=2,& D^{\prime }\left(a_2\right)=-1,\\ N\left(a_3\right)=5,& D^{\prime }\left(a_3\right)=2,\end{array}\\ {\mathcal{L}}^{-1}\left\{\frac{s^2+1}{s^3+3s^2+2s}\right\}=\frac{1}{2}-2e^{-t}+\frac{5}{2}{e}^{-2t}.\end{array}$$

Example2: Inverse Laplace Transform

To determine ${\mathcal{L}}^{-1}\left\{\frac{s}{s^2+4s+5}\right\}$, we first write

$$\frac{s}{s^2+4s+5}=\frac{s}{(s+2{)}^2+1}=\frac{(s+2)-2}{(s+2{)}^2+1}.$$

Pairs $(T25,26)$ then give the required inverse transform

$$e^{-2t}(\cos t-2\sin t).$$

Example3: Solving the following ODE with Laplace Transform

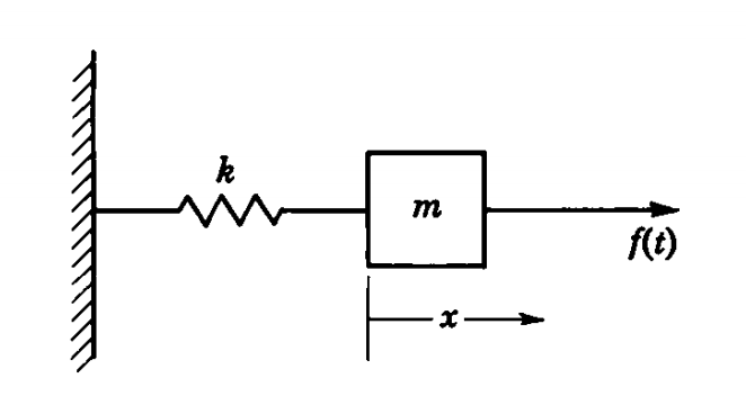
Forced vibration:

$$\begin{array}{c}m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}+kx=f(t)x(0)=\frac{\mathrm{d}x(0)}{\mathrm{d}t}=0\\ m{s}^2\overline{x}+k\overline{x}=\overline{f}.\end{array}$$

Thus, if we write

$${\omega }_0^2=\frac{k}{m},$$

the transform of the required solution is

$$\overline{x}=\frac{1}{m}\frac{\overline{f}}{s^2+{\omega }_0^2}.$$

Since $\frac{1}{s^2+{\omega }_0^2}$ is the transform of $\frac{\sin {\omega }_{0}t}{{\omega }_0}$, this product can be considered as the product of the transforms of $\frac{\sin {\omega }_{0}t}{m{\omega }_0}$ and $f(t)$, and hence use of the convolution (T10) gives the solution

$$x=\frac{1}{m{\omega }_0}{\int }_0^{t}f(u)\sin {\omega }_0(t-u)\mathrm{d}u$$

in terms of an arbitrary force function $f(t)$.

Example4: Solving the ODEs with Laplace Transform

We require the solution of the simultaneous equations

$$\begin{array}{l}\frac{\mathrm{d}x}{\mathrm{d}t}-y=e^t\\ \frac{\mathrm{d}y}{\mathrm{d}t}+x=\sin t\end{array}\}$$

which satisfies the conditions

$$x(0)=1,y(0)=0.$$

The transforms of equations satisfying initial conditions are

$$\begin{array}{l}s\overline{x}-\overline{y}=\frac{1}{s-1}+1\\ \overline{x}+s\overline{y}=\frac{1}{s^2+1}\end{array}\}$$

from which we obtain, algebraically,

$$\begin{array}{rl}& \overline{x}=\frac{s}{(s-1)(s^2+1)}+\frac{s}{s^2+1}+\frac{1}{{(s^2+1)}^2}\\ & \overline{y}=-\frac{1}{(s-1)(s^2+1)}-\frac{1}{s^2+1}+\frac{s}{{(s^2+1)}^2}\end{array}$$

If the first terms on the right-hand sides of these equations are expanded in partial fractions, there follows

$$\begin{array}{l}\overline{x}=\frac{1}{2}[\frac{1}{s-1}+\frac{1}{s^2+1}+\frac{s}{s^2+1}+\frac{2}{{(s^2+1)}^2}]\\ \overline{y}=\frac{1}{2}[-\frac{1}{s-1}-\frac{1}{s^2+1}+\frac{s}{s^2+1}+\frac{2s}{{(s^2+1)}^2}]\end{array}\}$$

and reference to Table 1 gives the required solution,

$$\begin{array}{l}x=\frac{1}{2}(e^t+2\sin t+\cos t-t\cos t)\\ y=\frac{1}{2}(-e^t-\sin t+\cos t+t\sin t)\end{array}\}.$$

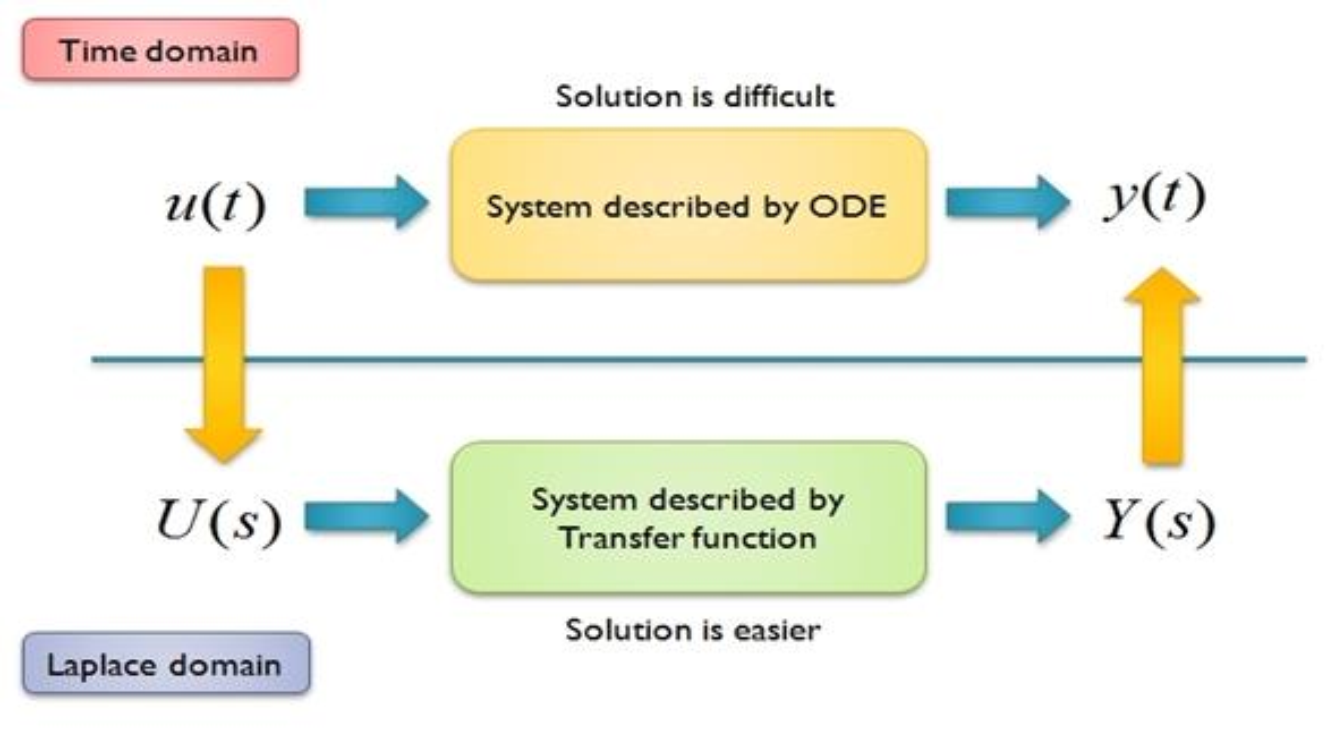
Laplace Transform: Beyond solving ODEs

The physical significance of Laplace Transform (LT): from time domain $s(t)$ to frequency domain $S(\omega )$