Introduction to Linear Partial Differential Equations*
This is the note from MNE8108 Engineering Methods in the Department of Mechanical Engineering, CityU (semester A, 2025)
Contents mostly From Advanced Calculus for Applications by Francis Begnaud Hildebrand
Partial differential equations definition
Motivation
Why do we study partial deferential equations (PDEs) and analytic solutions?
We are interested in PDEs because most of mathematical physics is described by such equations. For example, fluids dynamics (and more generally continuous media dynamics), electromagnetic theory, quantum mechanics and etc.
Typically, a given PDE will only be accessible to numerical solution and analytic solutions in a practical or research scenario are often impossible. However, it is vital to understand the general theory in order to conduct a sensible investigation. For example, we may need to understand what type of PDE we have to ensure the numerical solution is valid. Indeed, certain types of equations need appropriate boundary conditions; without a knowledge of the general theory it is possible that the problem may be ill-posed and the solution is erroneous.
Definition
Definition: Partial derivatives
Partial derivatives: The differential (or differential form) of a function
where the partial derivatives are defined by
A partial differential equation (PDE) is an equation for some quantity
Linear
The order of the PDE is the order of the highest (partial) differential coefficient in the equation.
As with ordinary differential equations (ODEs) it is important to be able to distinguish between linear and nonlinear equations.
A linear equation is one in which the equation and any boundary or initial conditions do not include any product of the dependent variables or their derivatives; an equation that is not linear is a nonlinear equation.
Principle of superposition: A linear equation has the useful property that if
Example of Linear PDEs: Wave Equations
Waves on a string, sound waves, waves on stretch membranes, electromagnetic waves, etc.
or more generally
where
Example of Linear PDEs: Heat Conduction
or more generally
or even
where
First Order Linear PDE: Method of Characteristic
We consider linear first order partial differential equation in two independent variables:
where
The key to the solution of the equation (2.1) is to find a change of variables (or a change of coordinates)
which transforms (2.1) into the simpler equation
where
We shall define this transformation so that it is one-to-one, at least for all
for
We substitute these into equation (2.1) to obtain
We can rearrange this as
This is close to the form of equation (2.1) if we can choose
Provided that
Then the equation is
Suppose we can define a new variable (or coordinate)
implies that
Equation (2.5) is called the characteristic equation of the linear equation (2.1). Its solution can be written in the form
So, we have made the coefficient of
Then
and we have already assumed this non-zero.
Now we see from equation (2.4) that this change of variables,
transforms equation (2.1) to
where
Finally, restricting the variables to a set in which
which is in the form of (2.3) with
The point of this transformation is that we can solve equation (2.3). Think of
as a linear first order ordinary differential equation in
Now we integrate with respect to
in which
We obtain the general form of the original equation by substituting back
Example: The method of characteristic
Example: Consider the constant coefficient equation
where
with general solution defined by the equation
So the characteristics of the PDE are the straight line graphs of
Using the substitution we find the equation transforms to
The integrating factor method gives
and integrating with respect to
where
and in terms of
Example 1: More specific Linear first order PDE
Consider
The characteristic equation is
and the characteristics are the straight line graphs 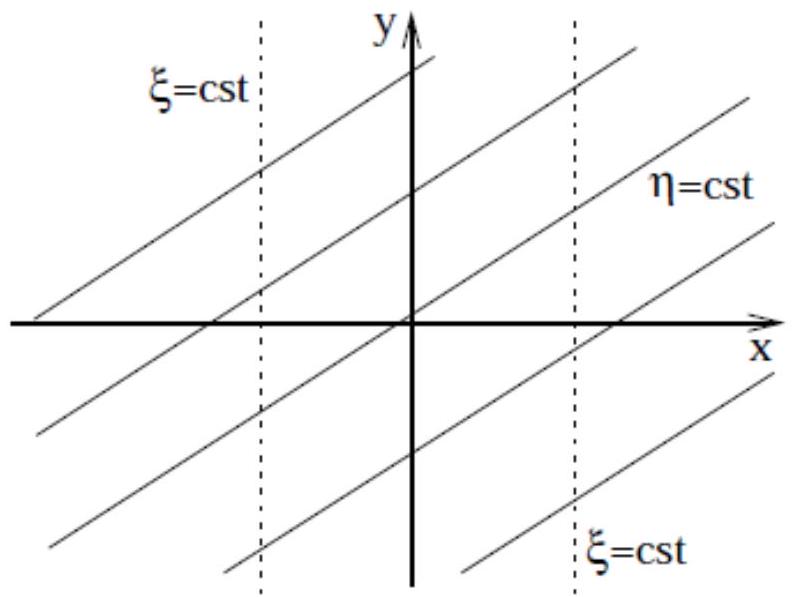
(We can see that an
This gives the solution
where
Suppose we specify values of
Then we need
and putting
This determines
We have determined the unique solution of the PDE with
to give the unique solution
satisfying
However, not every curve in the plane can be used to determine
Now we must choose
This requires
Last, we consider again
Now we must choose
This requires
Depending on the initial conditions, the PDE has one unique solution, no solution at all or an infinite number or solutions. The difference is that the
Example 2
Characteristics:
So, take
Finally the general solution is,
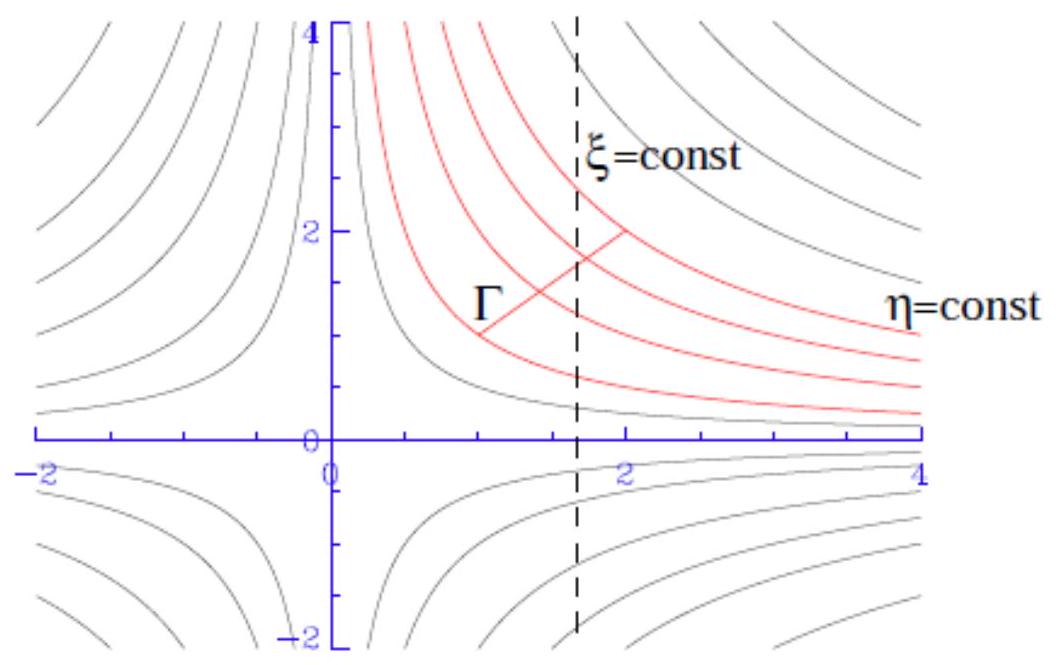
This figure presents the characteristic curves given by
Application: Linear Waves
If
The solution of the equation of characteristics,
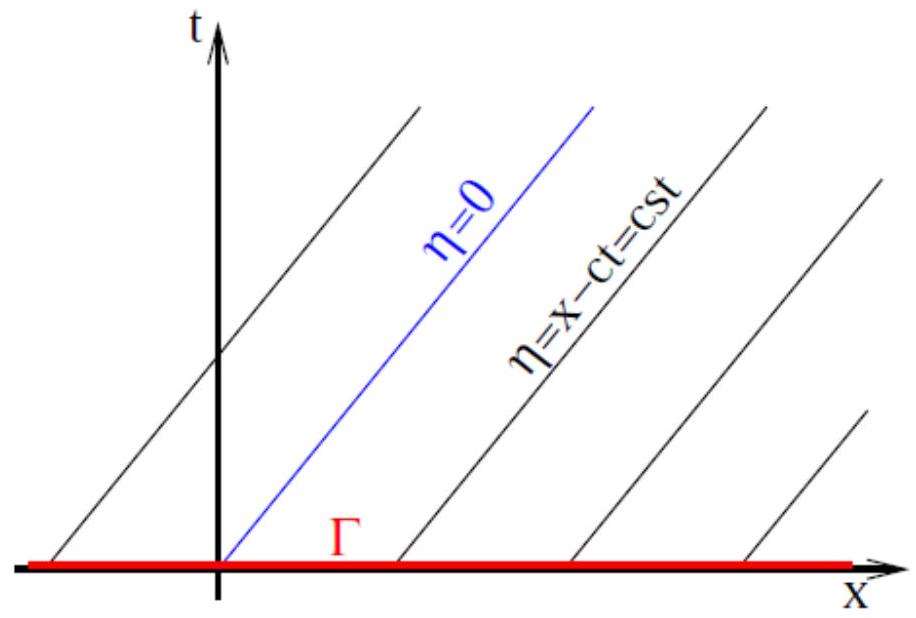
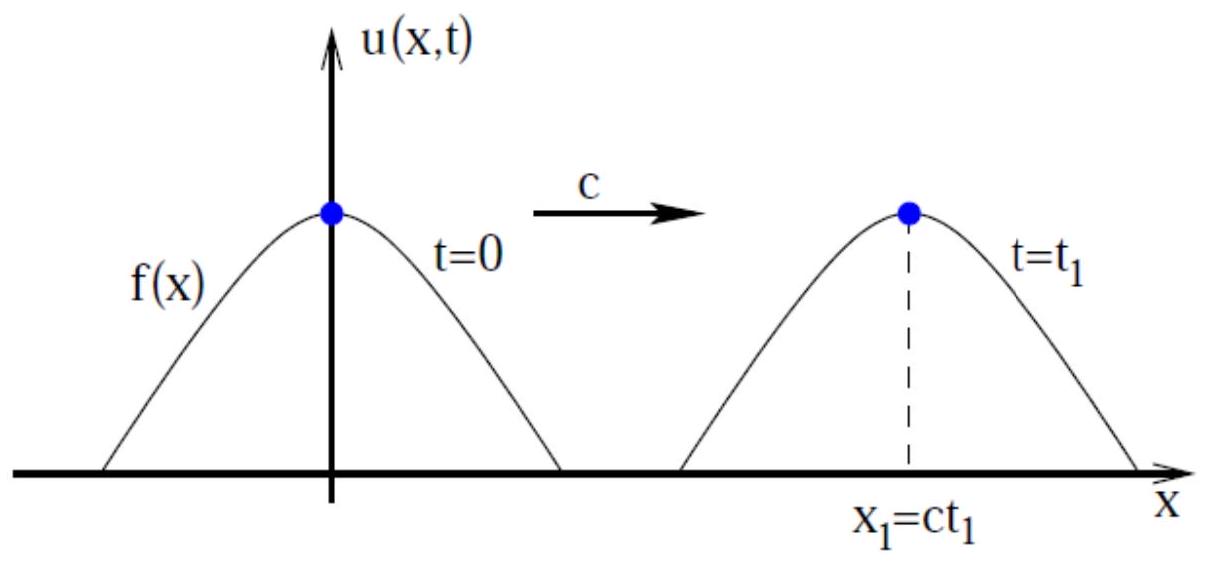
Note that
Second Order Linear PDE
Consider a general second order linear equation in two independent variables
Recall, for a first order linear and semilinear equation,
For the second order equation, can we also transform the variables from
As before we compute chain rule derivations
The equation becomes
where
Equation (3.1) can be simplified if we can choose
then we can write
Now consider the quadratic equation Vanish the item:
whose solution is given by
- If the discriminant
:
equation (3.2) has two distinct roots; so, we can make both coefficients
Then, using
Furthermore, if the discriminant
then
and make use of (3.3) to find that this characteristics satisfy
Similarly we find that the characteristic curves described by
- If the discriminant
:
equation (3.2) has one unique root and if we take this root for
To get
so that
Classification of
- If
we can apply the change of variable to transform the original PDE to
In this case the equation is said to be hyperbolic and has two families of characteristics given by equation (3.4) and equation (3.5).
- If
, a suitable choice for still simplifies the PDE, but now we can choose arbitrarily - provided and are independent - and the equation reduces to the form
The equation is said to be parabolic and has only one family of characteristics given by equation (3.6).
- If
we can again apply the change of variables to simplify the equation but now this functions will be complex conjugate. To keep the transformation real, we apply a further change of variables via
so, the equation can be reduced to
In this case the equation is said to be elliptic and has no real characteristics.
Example
- The wave equation,
is hyperbolic (
- The diffusion (heat conduction) equation,
is parabolic (
- Laplace's equation,
is elliptic
Example 1: Reduce to the canonical form
Here
We can choose
and the equation becomes
This has solution
where