Introduction of Linear algebra
This is the note from MNE8108 Engineering Methods in the Department of Mechanical Engineering, CityU (semester A, 2025)
Contents mostly From Linear Algebra by Arnold J. Insel etc.
Appendix A: Sets
Definitions
Definition: sets
collection of objects, called elements of the set
- list them using
- no order:
subsets:
- proper set:
- empty set:
calculation
union:
intersection:
- disjoint sets:
- disjoint sets:
finite sets:
infinite sets:
Number systems:
- Natural number:
- Integral number:
- Rational number:
- Real number:
- Complex number:
Cardinal number: the number if elements of a set
For infinite sets:
- Countable sets:
: - Uncountable sets: beth one:
operations
operation: from a set to itself
Unary:
- negation:
- factorial:
- trigonometric:
Binary:
tenary: ...
Arithmetic
Set Elements Operation Closure Associative Commutative Distributive - - Set Elements Operation Identity inverses or
More generally:
| Set | |||
|---|---|---|---|
| Elements | |||
| Operation | |||
| Closure | |||
| Associative | |||
| Commutative | |||
| Distributive | - | - | - |
| Identity | |||
| inverses |
group
Given:
- Set of elements
- Operation:
| Set | |
|---|---|
| Elements | |
| Operation | |
| Closure | |
| Associative | |
| Commutative | |
| Distributive | - |
| Identity | |
| inverses |
- If communtative: commutative group / abelian group
- If not commutative: non-commutative group / non-abelian group
Example of group:
commutative:
with commutes under
non-commutative:
- Dihedral group:
: rotation : reflection
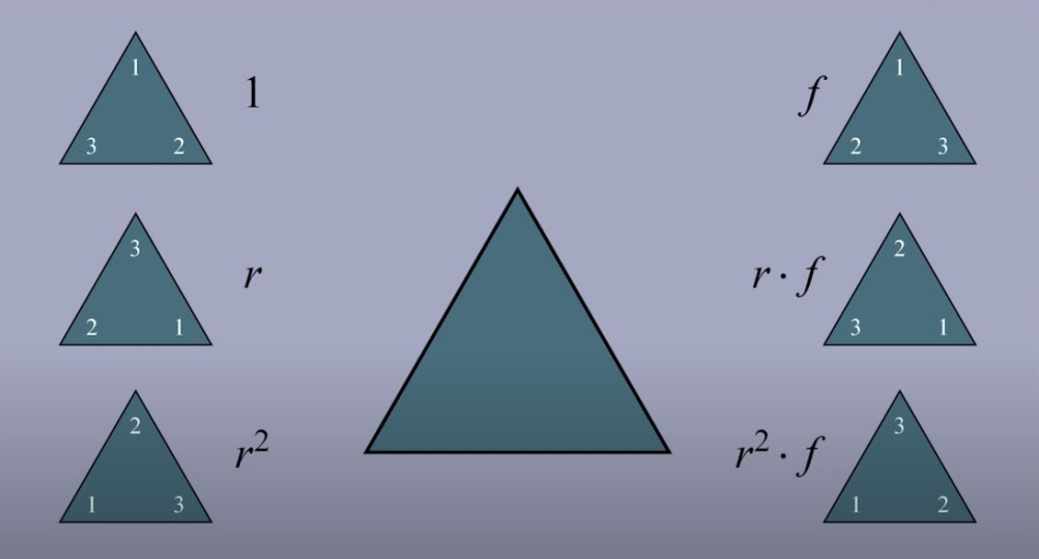
- Dihedral group:
Ring
Given:
- Set of elements
- Operation:
| Set | ||
|---|---|---|
| Elements | ||
| Operation | Addition | Multiplication |
| Closure | ||
| Associative | ||
| Commutative | ||
| Distributive | ||
| Identity | ||
| Inverses |
- distributive: left distributive v.s. right distributive
- If communitative, just check one distributivity
Example of ring:
- commutative:
with
- non-commutative:
with matrix addition and matrix multiplication
Appendix C: Fields
Given:
- Set of elements
- Operation:
| Set | |
|---|---|
| Elements | |
| Operation | Addition |
| Closure | |
| Associative | |
| Commutative | |
| Distributive | |
| Identity | |
| inverses |
Example of field:
with with with , a finite field with two elements(0,1); operations: XOR + AND.
Modulo Arithmetic:
Theorem C.1 (Cancellation Laws)
- If
, then - If
, then
Corollary
the identity elements and the inverse elements are unique
Theorem C.2
1.2 vector space
Given:
- Set of elements
- Operation:
- Commutative group
under , with a Field
| Set | ||||
|---|---|---|---|---|
| Elements | ||||
| Operation | Addition | Scalar multiplication | Addition | Multiplication |
| Closure | ||||
| Associative | ||||
| Commutative | ||||
| Distributive | - | |||
| Identity | ||||
| inverses |
Definition: vector space
A vector space
(Commutativity of addition); (Associativity for each ); - There exists an element in
denoted by s.t. ; , there exists an element , s.t. ; ; ; ;
Module definition: similar to vector space, but:
- commutative of scalar multiplication not required
- commutative of multiplication for number part, not required
Definition
- sum:
- product:
- scalars: elements of
- vectors: elements of vector space
- n-tuple:
elements of a field in this form: - entries / components:
- 2 n-tuples are equal if
: set of all n-tuples with entries from a field - vectors in
: column vectors
- entries / components:
Definition about some vector spaces
Definitions: Matrix
- diagonal entries:
with - i-th row:
- j-th column:
- zero matrix: all zero
- square: the number of rows and columns are equal
- equal:
- set of all
matrices with entries from a field is a vector space:
matrix addition:
Definitions: function
Let
for each
Definitions: polynominal
- coefficient:
- zero polynominal:
- degree:
for zero polynominal - largest exponent of
- equal if equal degree and
When
addition and scalar multiplication:
set of all polynominal:
Theorem 1.1: Cancellation Law for Vector Addition
If
Corolloary 1
The vector
Corolloary 2
The inverse element of vector is unique (additive inverse)
Theorem 1.2
In any vector space
1.3 subspace
Definition: subspace
A subset
In any vector space
Theorem 1.3(subspace)[core]
Let
. whenever and . whenever and .
Examples
matrix
The transpose
A symmetric matrix is a matrix
- Clearly, a symmetric matrix must be square. The set
of all symmetric matrices in is a subspace of since the conditions of Theorem 1.3 hold
A diagonal matrix is a
- the set of diagonal matrices is a subspace of
polynominal
Let
is a subspace of
theorem and definition
Theorem1.4
Any intersecton of subspaces of a vector space
Definitions
sum of nonempty subsets
direct sum:
are subspaces of
1.4 linear combination and systems of linear equations
Definition: linear combination
Let
Observe that in any vector space
Definition: span
Let
In
Theorem 1.5(span and subspace)
- The span of any subset
of a vector space is a subspace of . - Any subspace of
that contains must also contain the span of
Definition: generate
A subset
1.5 linear dependence and linear independence
Definition: linear independent
A subset
In this case we also say that the vectors of
For any vectors
Thus, for a set to be linearly dependent, there must exists a nontrivial representation of
Consequently, any subset of a vector space that contains the zero vector is linearly dependent because
Definition: linearly independent
A subset
The following facts about linearly independent sets are true in any vector space:
- The empty set is linearly independent, for linearly dependent sets must be nonempty.
- A set consisting of a single nonzero vector is linearly independent. For if
is linearly dependent. then for some nonzero scalar . Thus
- A set is linearly independent iff the only representations of
as linear combinations of its vectors are trivial representations
Examples
polynominal
For
is linearly independent in
theorem
Theorem 1.6
Let
linearly dependent, then
Corollary
Let
Theorem 1.7
Let
1.6 bases and dimension
basis
Definition: basis [core]
A basis
Examples
Recalling that
and is linearly independent, we see that is a basis for the zero vector space. In
, let is readily seen to be a basis for
and is called the standard basis for . In
, let denote the matrix whose only nonzero entry is a in the ith row and jth column. Then is a basis for . In
the set is a basis. We call this basis the standard basis for .
Theorem
Theorem 1.8:
Let
for unique scalars
Theorem 1.9
If a vector space
Theorem 1.10(Replacement Theorem)
Let
Corollary 1
Let
dimension
Definitions: dimension [core]
A vector space is called finite-dimensional if it has a basis consisting of a finite number of vectors. The unique number of vectors in each basis for
Examples
- The vector space
has dimension - The vector space
has dimension - The vector space
has dimension - The vector space
has dimension
The following examples show that the dimension of a vector space depends on its field of scalars.
- Over the field of complex numbers, the vector space of complex numbers has dimension
. (A basis is .) - Over the field of real numbers, the vector space of complex numbers has dimension
. (A basis is )
Corollary and theorem
Corollary 2
Let
- Any finite generating set for
contains at least vectors, and a generating set for that contains exactly vectors is a basis for . - Any linearly independent subset of
that contains exactly is vectors is a basis for . - Every linearly independent subset of
can be extended to a basis for .
Theorem 1.11:
Let
Examples
The set of diagonal
where
Corollary
If